Question

【题目】如图，已知离心率为 的椭圆 过点M（2，1），O为坐标原点，平行于OM的直线i交椭圆C于不同的两点A、B．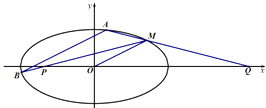
（1）求椭圆C的方程；
（2）记直线MB、MA与x轴的交点分别为P、Q，若MP斜率为k1 ， MQ斜率为k2 ， 求k1+k2 ．

Answer 1

【答案】
（1）解：设椭圆C的方程为： ．

由题意得： ，

把①代入②得：a2=4b2④．

联立③④得：a2=8，b2=2．

∴椭圆方程为

（2）解：∵M（2，1），∴kOM=

又∵直线l∥OM，可设l：y= x+m，将式子代入椭圆C得：x2+4（ x+m）2﹣8=0，

整理得：x2+2mx+2m2﹣4=0．

设A（x1，y1），B（x2，y2），则x1+x2=﹣2m，x1x2=2m2﹣4．

设直线MA、MB的斜率分别为k1、k2，则k1= ，k2= ．

事实上，k1+k2= +

= =1+m（ + ）

=1+m

=1+m

=1﹣

=0．

k1+k2的值为0

【解析】（1）由给出的椭圆的离心率、椭圆过定点M（2，1）及隐含条件a2=b2+c2列方程组可求a2 ， b2 ， 则椭圆方程可求；（2）设出直线l的方程，设出A，B两点的坐标，把直线和椭圆联立后可求A，B两点的横坐标的和与积，把直线MA，MB的斜率k1、k2分别用A，B两点的坐标表示，把纵坐标转化为横坐标后，则k1+k2仅含A，B两点的横坐标的和与积，化简整理即可得到结论．