题目内容
【题目】2012年，商品价格一度成为社会热点话题，某种新产品投放市场的100天中，前40天价格呈直线上升，由于政府及时采取有效措施，从而使后60天的价格呈直线下降，现统计出其中4天的价格如下表
时间 | 第4天 | 第32天 | 第60天 | 第90天 |
价格（元） | 23 | 30 | 22 | 7 |
（1）写出价格f（x）关于时间x的函数关系式（x表示投放市场的第x天）；
（2）销售量g（x）与时间x的函数关系： 
（1≤x≤100，且x∈N），则该产品投放市场第几天销售额最高？最高为多少元？
【答案】
（1）解：由题意知，当1≤x＜40时，一次函数y=ax+b过点A（4，23），B（32，30），代入函数求得a= 
，b=22；
当40≤x≤100时，一次函数y=kx+m过点C（60，22），D（90，7），代入函数求得k=﹣ 
，m=52；
∴函数解析式为：y=f（x）=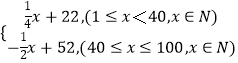 
（2）解：设日销售额为S千元，当1≤x＜40时，S（x）=（ x+22）（﹣ 
x+ 
）=﹣ 
（x﹣ 
）2+ 
；
∴当x=10或11时，函数有最大值S（x）max= 
=808.5（千元）；
当40≤x≤100时，S（x）=（﹣ x+52）（﹣ x+ ）= 
（x2﹣213x+11336）；
∴当x=40时，s（x）max=736（千元）．
综上所知，日销售额最高是在第10天或第11天，最高值为808.5千元
【解析】（1）价格直线上升，直线下降，说明价格函数f（x）是一次函数，由表中对应关系用待定系数法易求f（x）的表达式；（2）由销售额=销售量×时间，得日销售额函数S（x）的解析式，从而求出S（x）的最大值．
【考点精析】本题主要考查了函数的值域的相关知识点，需要掌握求函数值域的方法和求函数最值的常用方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的才能正确解答此题．
