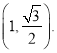题目内容
【题目】如图，在等腰梯形ABCD中，AB∥CD，且AB=2AD，设∠DAB=θ，θ∈（0， 
），以A，B为焦点且过点D的双曲线的离心率为e1 ， 以C，D为焦点且过点A的椭圆的离心率为e2 ， 则（ ） 
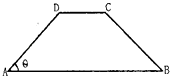
A.随着角度θ的增大，e1增大，e1e2为定值
B.随着角度θ的增大，e1减小，e1e2为定值
C.随着角度θ的增大，e1增大，e1e2也增大
D.随着角度θ的增大，e1减小，e1e2也减小
【答案】B
【解析】解：连接BD，AC 设AD=t，
则BD= 
= 
∴双曲线中a= 
e1= 
∵y=cosθ在（0， 
）上单调减，进而可知当θ增大时，y= = 
减小，即e1减小
∵AC=BD
∴椭圆中CD=2t（1﹣cosθ）=2c∴c'=t（1﹣cosθ）
AC+AD= +t，∴a'= 
（ +t）
e2= 
= 
∴e1e2= × =1
故选B．
练习册系列答案
阅读快车系列答案
相关题目
