题目内容
【题目】几年来，网上购物风靡，快递业迅猛发展，某市的快递业务主要由两家快递公司承接，即圆通公司与申通公司：“快递员”的工资是“底薪+送件提成”：这两家公司对“快递员”的日工资方案为：圆通公司规定快递员每天底薪为70元，每送件一次提成1元；申通公司规定快递员每天底薪为120元，每日前83件没有提成，超过83件部分每件提成10元，假设同一公司的快递员每天送件数相同，现从这两家公司各随机抽取一名快递员并记录其100天的送件数，得到如下条形图：
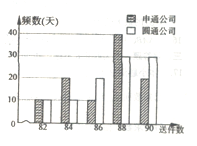
（1）求申通公司的快递员一日工资
（单位：元）与送件数
的函数关系；
（2）若将频率视为概率，回答下列问题：
①记圆通公司的“快递员”日工资为
（单位：元），求
的分布列和数学期望；
②小王想到这两家公司中的一家应聘“快递员”的工作，如果仅从日收入的角度考虑，请你利用所学过的统计学知识为他作出选择，并说明理由.
【答案】（1）
；（2）见解析.
【解析】试题分析：（1）可根据申通公司的快递员一日不同的工作量，分段列出申通公司的快递员一日工资
（单位：元）与送件数
的函数关系；（2）①根据条形图可知X的所有可能取值为152,154,156,158,160，根据古典概型概率公式求出对应概率，即可得结果；②再算出申通公司的日工资的期望值，与圆通公司进行比较即可得结论.
试题解析：(1)由题意:当0≤n≤83时,y=120元,当n>85时,y=120+(n-83)×10=10n-710
∴申通公司的快递员一日工资y(单位：元)与送件数n的函数关系为:
y= 
(2)X的所有可能取值为152,154,156,158,160
①由题意:P(X=152)=0.1, P(X=154)=0.1, P(X=156)=0.2, P(X=158)=0.3, P(X=160)=0.3
∴ X的分布列为:
X | 152 | 154 | 156 | 158 | 160 |
P | 0.1 | 0.1 | 0.2 | 0.3 | 0.3 |
∴ X的数学期望EX=152×0.1+154×0.1+156×0.2+158×0.3+160×0.3=157.2(元)
②设申通公司的日工资为Y,则
EY=120+0×0.1+10×0.2+30×0.1+50×0.4+70×0.2=159(元)
由于到圆通公司的日工资的数学期望(均值)没有申通公司的日工资的数学期望(均值)高,所以小王应当到申通公司应聘“快递员”的工作.
