题目内容
14.已知函数f(x)=nx-xn,x∈R,其中n∈N•,且n≥2.(Ⅰ)讨论f(x)的单调性;
(Ⅱ)设曲线y=f(x)与x轴正半轴的交点为P,曲线在点P处的切线方程为y=g(x),求证:对于任意的正实数x,都有f(x)≤g(x);
(Ⅲ)若关于x的方程f(x)=a(a为实数)有两个正实数根x1,x2,求证:|x2-x1|<$\frac{a}{1-n}$+2.
分析 (Ⅰ)由f(x)=nx-xn,可得f′(x),分n为奇数和偶数两种情况利用导数即可得函数的单调性.
(Ⅱ)设点P的坐标为(x0,0),则可求x0=n${\;}^{\frac{1}{n-1}}$,f′(x0)=n-n2,可求g(x)=f′(x0)(x-x0),F′(x)=f′(x)-f′(x0).由f′(x)=-nxn-1+n在(0,+∞)上单调递减,可求F(x)在∈(0,x0)内单调递增,在(x0,+∞)上单调递减,即可得证.
(Ⅲ)设x1≤x2,设方程g(x)=a的根为${x}_{2}^{′}$,由(Ⅱ)可得x2≤${x}_{2}^{′}$.设曲线y=f(x)在原点处的切线方程为y=h(x),可得h(x)=nx,设方程h(x)=a的根为${x}_{1}^{′}$,可得${x}_{1}^{′}$<x1,从而可得:x2-x1<${x}_{2}^{′}$-${x}_{1}^{′}$=$\frac{a}{1-n}+{x}_{0}$,由n≥2,即2n-1=(1+1)n-1≥1+${C}_{n-1}^{1}$=1+n-1=n,推得:2$≥{n}^{\frac{1}{n-1}}$=x0,即可得证.
解答 (本题满分为14分)
解:(Ⅰ)由f(x)=nx-xn,可得f′(x)=n-nxn-1=n(1-xn-1),其中n∈N•,且n≥2.
下面分两种情况讨论:
(1)当n为奇数时,令f′(x)=0,解得x=1,或x=-1,当x变化时,f′(x),f(x)的变化情况如下表:
| x | (-∞,-1) | (-1,1) | (1,+∞) |
| f′(x) | - | + | - |
| f(x) |  |  |  |
(2)当n为偶数时,
当 f′(x)>0,即x<1时,函数 f(x)单调递增;
当 f′(x)<0,即x>1时,函数 f(x)单调递减;
所以,f(x)在(-∞,1)单调递增,在(1,+∞)上单调递减;
(Ⅱ)证明:设点P的坐标为(x0,0),则x0=n${\;}^{\frac{1}{n-1}}$,f′(x0)=n-n2,
曲线y=f(x)在点P处的切线方程为y=f′(x0)(x-x0),即g(x)=f′(x0)(x-x0),
令F(x)=f(x)-g(x),即F(x)=f(x)-f′(x0)(x-x0),则F′(x)=f′(x)-f′(x0).
由于f′(x)=-nxn-1+n在(0,+∞)上单调递减,故F′(x)在(0,+∞)上单调递减,
又因为F′(x0)=0,所以当x∈(0,x0)时,F′(x)>0,当x∈(x0,+∞)时,F′(x)<0,
所以F(x)在∈(0,x0)内单调递增,在(x0,+∞)上单调递减,
所以对应任意的正实数x,都有F(x)≤F(x0)=0,
即对于任意的正实数x,都有f(x)≤g(x).
(Ⅲ)证明:不妨设x1≤x2,
由(Ⅱ)知g(x)=(n-n2)(x-x0),
设方程g(x)=a的根为${x}_{2}^{′}$,可得${x}_{2}^{′}$=$\frac{a}{n-{n}^{2}}+{x}_{0}$,
由(Ⅱ)知g(x2)≥f(x2)=a=g(${x}_{2}^{′}$),可得x2≤${x}_{2}^{′}$.
类似地,设曲线y=f(x)在原点处的切线方程为y=h(x),
可得h(x)=nx,当x∈(0,+∞),f(x)-h(x)=-xn<0,
即对于任意的x∈(0,+∞),f(x)<h(x),
设方程h(x)=a的根为${x}_{1}^{′}$,可得${x}_{1}^{′}$=$\frac{a}{n}$,
因为h(x)=nx在(-∞,+∞)上单调递增,且h(${x}_{1}^{′}$)=a=f(x1)<h(x1),
因此${x}_{1}^{′}$<x1,
由此可得:x2-x1<${x}_{2}^{′}$-${x}_{1}^{′}$=$\frac{a}{1-n}+{x}_{0}$,
因为n≥2,所以2n-1=(1+1)n-1≥1+${C}_{n-1}^{1}$=1+n-1=n,
故:2$≥{n}^{\frac{1}{n-1}}$=x0.
所以:|x2-x1|<$\frac{a}{1-n}$+2.
点评 本题主要考查导数的运算、导数的几何意义、利用导数研究函数的性质、证明不等式等基础知识和方法,考查分类讨论思想、函数思想和化归思想,考查综合分析问题和解决问题的能力.

练习册系列答案
相关题目
4.设集合M={x|x2=x},N={x|lgx≤0},则M∪N=( )
| A. | [0,1] | B. | (0,1] | C. | [0,1) | D. | (-∞,1] |
2.阅读如图的程序框图,运行相应的程序,则输出S的值为( )
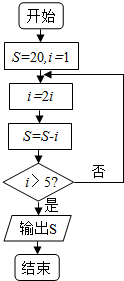

| A. | -10 | B. | 6 | C. | 14 | D. | 18 |
19.设A,B是有限集,定义:d(A,B)=card(A∪B)-card(A∩B),其中card(A)表示有限集A中的元素个数( )
命题①:对任意有限集A,B,“A≠B”是“d(A,B)>0”的充分必要条件;
命题②:对任意有限集A,B,C,d(A,C)≤d(A,B)+d(B,C)
命题①:对任意有限集A,B,“A≠B”是“d(A,B)>0”的充分必要条件;
命题②:对任意有限集A,B,C,d(A,C)≤d(A,B)+d(B,C)
| A. | 命题①和命题②都成立 | B. | 命题①和命题②都不成立 | ||
| C. | 命题①成立,命题②不成立 | D. | 命题①不成立,命题②成立 |
5.从1,2,3,4,5中有放回的依次取出两个数,则下列各对事件中是互斥事件的是( )
| A. | 恰有1个是奇数和全是奇数 | B. | 恰有1个是偶数和至少有1个是偶数 | ||
| C. | 至少有1个是奇数和全是奇数 | D. | 至少有1个是偶数和全是偶数 |
6.如果3个正整数可作为一个直角三角形三条边的边长,则称这3个数为一组勾股数.从1,2,3,4,5中任取3个不同的数,则这3个数构成一组勾股数的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{20}$ |