题目内容
6.如果3个正整数可作为一个直角三角形三条边的边长,则称这3个数为一组勾股数.从1,2,3,4,5中任取3个不同的数,则这3个数构成一组勾股数的概率为( )| A. | $\frac{3}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{20}$ |
分析 一一列举出所有的基本事件,再找到勾股数,根据概率公式计算即可.
解答 解:从1,2,3,4,5中任取3个不同的数,有(1,2,3),(1,2,4),(1,2,5),(1,3,4),(1,3,5),(1,4,5)(2,3,4),(2,3,5),(2,4,5),(3,4,5)共10种,
其中只有(3,4,5)为勾股数,
故这3个数构成一组勾股数的概率为$\frac{1}{10}$.
故选:C
点评 本题考查了古典概型概率的问题,关键是不重不漏的列举出所有的基本事件,属于基础题.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
15.已知集合A={1,2,3},B={2,3},则( )
| A. | A=B | B. | A∩B=∅ | C. | A$\stackrel{?}{≠}$B | D. | B$\stackrel{?}{≠}$A |
16.某学校为了了解三年级、六年级、九年级这三个年级之间的学生视力是否存在显著差异,拟从这三个年级中按人数比例抽取部分学生进行调查,则最合理的抽样方法是( )
| A. | 抽签法 | B. | 系统抽样法 | C. | 分层抽样法 | D. | 随机数法 |
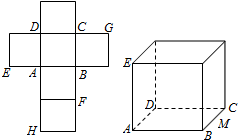 一个正方体的平面展开图及该正方体的直观图的示意图如图所示.在正方体中,设BC的中点为M、GH的中点为N.
一个正方体的平面展开图及该正方体的直观图的示意图如图所示.在正方体中,设BC的中点为M、GH的中点为N.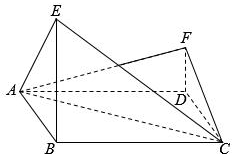 如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面 ABCD,BE=2DF,AE丄EC.
如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面 ABCD,BE=2DF,AE丄EC.