题目内容
已知函数f(x)=a-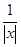 .
.
(1)求证:函数y=f(x)在(0,+∞)上是增函数;
(2)若f(x)<2x在(1,+∞)上恒成立,求实数a的取值范围.
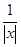 .
.(1)求证:函数y=f(x)在(0,+∞)上是增函数;
(2)若f(x)<2x在(1,+∞)上恒成立,求实数a的取值范围.
(1)见解析 (2)(-∞,3]
解:(1)证明:当x∈(0,+∞)时,
f(x)=a-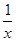 ,
,
设0<x1<x2,则x1x2>0,x2-x1>0,
f(x2)-f(x1)=(a-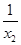 )-(a-
)-(a-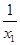 )=
)=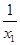 -
-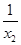 =
= >0,
>0,
∴f(x)在(0,+∞)上是增函数.
(2)由题意:a-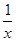 <2x在(1,+∞)上恒成立,
<2x在(1,+∞)上恒成立,
设h(x)=2x+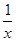 ,
,
则a<h(x)在(1,+∞)上恒成立.
任取x1,x2∈(1,+∞)且x1<x2,
h(x1)-h(x2)=(x1-x2)(2-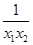 ).
).
∵1<x1<x2,∴x1-x2<0,x1x2>1,
∴2-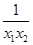 >0,∴h(x1)<h(x2),
>0,∴h(x1)<h(x2),
∴h(x)在(1,+∞)上单调递增.
故a≤h(1)即a≤3,
∴a的取值范围是(-∞,3].
f(x)=a-
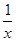 ,
,设0<x1<x2,则x1x2>0,x2-x1>0,
f(x2)-f(x1)=(a-
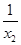 )-(a-
)-(a-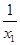 )=
)=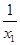 -
-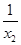 =
= >0,
>0,∴f(x)在(0,+∞)上是增函数.
(2)由题意:a-
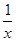 <2x在(1,+∞)上恒成立,
<2x在(1,+∞)上恒成立,设h(x)=2x+
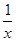 ,
,则a<h(x)在(1,+∞)上恒成立.
任取x1,x2∈(1,+∞)且x1<x2,
h(x1)-h(x2)=(x1-x2)(2-
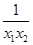 ).
).∵1<x1<x2,∴x1-x2<0,x1x2>1,
∴2-
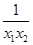 >0,∴h(x1)<h(x2),
>0,∴h(x1)<h(x2),∴h(x)在(1,+∞)上单调递增.
故a≤h(1)即a≤3,
∴a的取值范围是(-∞,3].

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
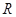 上的奇函数
上的奇函数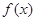 ,当
,当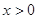 时,
时,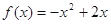
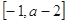 上单调递增,求实数
上单调递增,求实数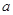 的取值范围。
的取值范围。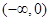 上单调递增的是( )
上单调递增的是( )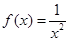
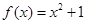
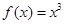
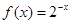
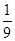 ,则f(x)的单调递减区间是( )
,则f(x)的单调递减区间是( )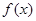 为定义域在R上的偶函数,且
为定义域在R上的偶函数,且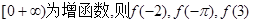 的大小顺序为( )
的大小顺序为( ) 
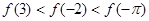

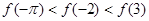
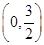 时,f(x)=ln(x2-x+1),则函数f(x)在区间[0,6]上的零点个数为( )
时,f(x)=ln(x2-x+1),则函数f(x)在区间[0,6]上的零点个数为( )