题目内容
12.M为抛物线y2=8x上一点,F为抛物线的焦点,∠MFO=120°(O为坐标原点),N(-2,0),则直线MN的斜率为( )| A. | $±\frac{1}{3}$ | B. | ±$\frac{1}{2}$ | C. | ±$\frac{\sqrt{3}}{2}$ | D. | ±$\frac{\sqrt{2}}{2}$ |
分析 利用cos120°=$\frac{\overrightarrow{FM}•\overrightarrow{FO}}{|\overrightarrow{FM}|•|\overrightarrow{FO}|}$计算可得M(6,$±4\sqrt{3}$),进而可得结论.
解答 解:设M($\frac{1}{8}{y}^{2}$,y),由题可知F(2,0),
∴$\overrightarrow{FM}$=($\frac{1}{8}{y}^{2}$-2,y),$\overrightarrow{FO}$=(-2,0),
∴cos120°=$\frac{\overrightarrow{FM}•\overrightarrow{FO}}{|\overrightarrow{FM}|•|\overrightarrow{FO}|}$=$\frac{4-\frac{1}{4}{y}^{2}}{2•(2+\frac{1}{8}{y}^{2})}$=-$\frac{1}{2}$,
解得y=±4$\sqrt{3}$,∴M(6,$±4\sqrt{3}$),
又∵N(-2,0),∴kMN=$\frac{±4\sqrt{3}}{6-(-2)}$=$±\frac{\sqrt{3}}{2}$,
故选:C.
点评 本题考查抛物线中直线的斜率,注意解题方法的积累,属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
3.某市对汽车限购政策进行了调查,在参加调查的300名有车人中116名持反对意见,200名无车人中有121名持反对意见,在运用这些数据说明“拥有车辆”与“反对汽车限购政策”是否有关系时,最有说服力的方法是( )
| A. | 平均数与方差 | B. | 回归直线方程 | C. | 独立性检验 | D. | 概率 |
20.已知M=$\int_0^1{\frac{1}{x+1}dx,N=\int_0^{\frac{π}{2}}{cosxdx}}$,由图示程序框图输出的S为( )
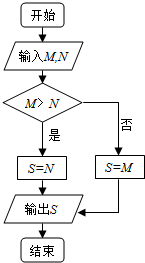

| A. | 1 | B. | ln2 | C. | $\frac{π}{2}$ | D. | 0 |
7.若复数z满足iz=2+4i,则z在复平面内对应的点的坐标是( )
| A. | (4,2) | B. | (2,-4) | C. | (2,4) | D. | (4,-2) |
1.已知集合M={1,2,3,5,7},N={x|x=2k-1,k∈M},则M∩N=( )
| A. | {1,2,3} | B. | {1,3,5} | C. | {2,3,5} | D. | {1,3,5,7} |
 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,M、N分别是这段图象的最高点和最低点,且$\overrightarrow{OM}•\overrightarrow{ON}$=0(O为坐标原点),则A=$\frac{\sqrt{7}}{12}$π.
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,M、N分别是这段图象的最高点和最低点,且$\overrightarrow{OM}•\overrightarrow{ON}$=0(O为坐标原点),则A=$\frac{\sqrt{7}}{12}$π.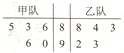 某项比赛规则是:先进行个人赛,每支参赛队的成绩前三名队员再代表本队进行团体赛,团体赛是在两队名次相同队员之间进行且三场比赛同时进行.根据以往比赛统计:两名队员中个人赛成绩高的队员在各场获胜的概率为$\frac{2}{3}$,负的概率为$\frac{1}{3}$,且各场比赛互不影响.已知甲乙队各5名队员,这10名队员的个人赛成绩如图所示:
某项比赛规则是:先进行个人赛,每支参赛队的成绩前三名队员再代表本队进行团体赛,团体赛是在两队名次相同队员之间进行且三场比赛同时进行.根据以往比赛统计:两名队员中个人赛成绩高的队员在各场获胜的概率为$\frac{2}{3}$,负的概率为$\frac{1}{3}$,且各场比赛互不影响.已知甲乙队各5名队员,这10名队员的个人赛成绩如图所示: