题目内容
(本小题满分14分) 已知中心在坐标原点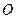 的椭圆
的椭圆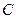 经过点
经过点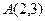 ,且点
,且点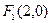 为其右焦点。
为其右焦点。
(1)求椭圆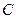 的方程;
的方程;
(2)是否存在平行于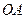 的直线
的直线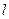 ,使得直线
,使得直线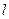 与椭圆
与椭圆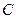 有公共点,且直线
有公共点,且直线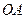 与
与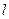 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
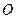 的椭圆
的椭圆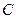 经过点
经过点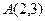 ,且点
,且点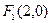 为其右焦点。
为其右焦点。(1)求椭圆
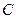 的方程;
的方程;(2)是否存在平行于
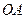 的直线
的直线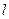 ,使得直线
,使得直线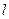 与椭圆
与椭圆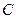 有公共点,且直线
有公共点,且直线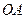 与
与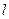 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。(1)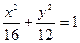 ;
;
(2)直线 不存在
不存在
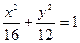 ;
;(2)直线
 不存在
不存在(1)依题意,可设椭圆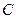 的方程为
的方程为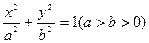 ,且可知左焦点为
,且可知左焦点为
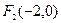 ,从而有
,从而有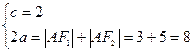 ,解得
,解得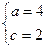 ………4分
………4分
又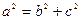 ,所以
,所以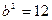 ,故椭圆
,故椭圆 的方程为
的方程为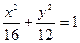 ………6分
………6分
(2)假设存在符合题意的直线 ,其方程为
,其方程为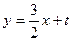 ………7分
………7分
由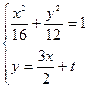 得
得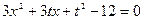 ,………9分
,………9分
因为直线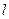 与椭圆
与椭圆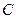 有公共点,所以有
有公共点,所以有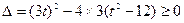 ,
,
解得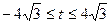 ………10分W$w
………10分W$w
另一方面,由直线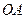 与
与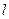 的距离为4可得
的距离为4可得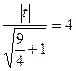 ,从而
,从而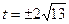 ………12分
………12分
由于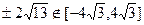 ,所以符合题意的直线
,所以符合题意的直线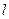 不存在。………14分
不存在。………14分
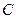 的方程为
的方程为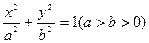 ,且可知左焦点为
,且可知左焦点为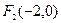 ,从而有
,从而有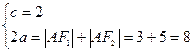 ,解得
,解得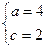 ………4分
………4分又
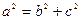 ,所以
,所以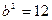 ,故椭圆
,故椭圆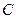 的方程为
的方程为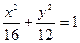 ………6分
………6分(2)假设存在符合题意的直线
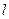 ,其方程为
,其方程为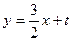 ………7分
………7分由
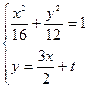 得
得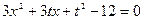 ,………9分
,………9分因为直线
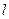 与椭圆
与椭圆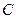 有公共点,所以有
有公共点,所以有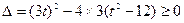 ,
,解得
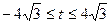 ………10分W$w
………10分W$w另一方面,由直线
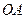 与
与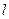 的距离为4可得
的距离为4可得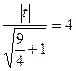 ,从而
,从而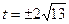 ………12分
………12分由于
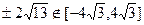 ,所以符合题意的直线
,所以符合题意的直线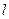 不存在。………14分
不存在。………14分
练习册系列答案
相关题目
 与圆
与圆 相交于
相交于 两点,
两点, 为坐标原点,
为坐标原点, 的面积为
的面积为 .
. 的函数
的函数 ,并求出其定义域;
,并求出其定义域;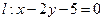 与圆
与圆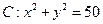 .
.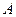 ,
,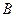 的坐标;
的坐标; 的面积。
的面积。 经过
经过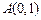 ,
,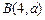
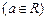 两点
两点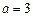 ,并且
,并且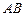 是圆
是圆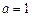 时,圆
时,圆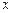 轴相切,求此时圆
轴相切,求此时圆 取何实数,圆
取何实数,圆 外的另一个定点,求出这个定点坐标
外的另一个定点,求出这个定点坐标 :
: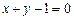 被圆C:
被圆C: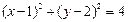 截得的弦长为
截得的弦长为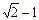
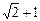
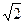
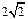
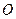 的直径
的直径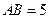 ,
,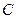 为圆周上一点,
为圆周上一点,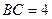 ,过点
,过点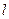 ,过点
,过点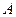 作
作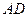 ,垂足为
,垂足为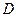 ,则
,则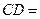 ____.
____.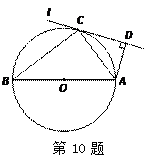
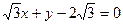 截圆
截圆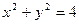 得到的劣弧所对的圆心角为 ( )
得到的劣弧所对的圆心角为 ( )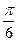
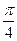
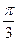
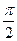
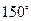 的直线被圆
的直线被圆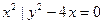 截得的弦长为 。
截得的弦长为 。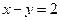 被圆
被圆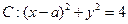 所截得的弦长为2
所截得的弦长为2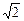 ,则实数a的值为
,则实数a的值为