题目内容
(本小题满分16分
已知圆 经过
经过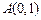 ,
,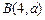
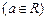 两点
两点
(1)当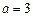 ,并且
,并且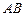 是圆
是圆 的直径,求此时圆
的直径,求此时圆 的标准方程
的标准方程
(2)当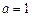 时,圆
时,圆 与
与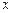 轴相切,求此时圆
轴相切,求此时圆 的方程
的方程
(3)如果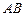 是圆
是圆 的直径,证明:无论
的直径,证明:无论 取何实数,圆
取何实数,圆 恒经过除
恒经过除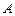 外的另一个定点,求出这个定点坐标
外的另一个定点,求出这个定点坐标
已知圆
 经过
经过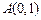 ,
,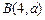
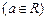 两点
两点(1)当
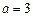 ,并且
,并且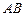 是圆
是圆 的直径,求此时圆
的直径,求此时圆 的标准方程
的标准方程(2)当
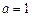 时,圆
时,圆 与
与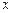 轴相切,求此时圆
轴相切,求此时圆 的方程
的方程(3)如果
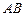 是圆
是圆 的直径,证明:无论
的直径,证明:无论 取何实数,圆
取何实数,圆 恒经过除
恒经过除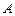 外的另一个定点,求出这个定点坐标
外的另一个定点,求出这个定点坐标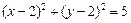
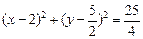
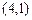
(1)圆心坐标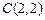 , (2分)
, (2分) 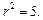 (4分) 方程
(4分) 方程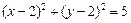 .(6分)
.(6分)
(2)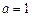 时,圆过
时,圆过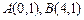 ,设圆的半径为
,设圆的半径为 则圆心为
则圆心为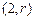 . (8分)
. (8分)
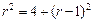 ,
, 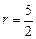 .(10分)
.(10分)
圆的方程为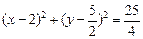 .(11分)
.(11分)
(3) 【法一】动圆的方程为: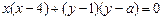 ,(13分) 则
,(13分) 则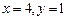 ,(14分)
,(14分)
等式恒成立.定点为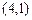 .(16分)
.(16分)
【法二】直径所对的圆周角为直角,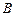 点在直线
点在直线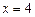 上运动.(13分)
上运动.(13分)
过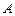 点作
点作 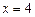 的垂线,垂足为
的垂线,垂足为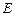 ,则
,则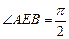 ,(14分)则圆恒过点
,(14分)则圆恒过点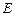
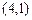 .(16分)
.(16分)
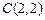 , (2分)
, (2分) 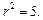 (4分) 方程
(4分) 方程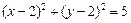 .(6分)
.(6分)(2)
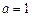 时,圆过
时,圆过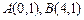 ,设圆的半径为
,设圆的半径为 则圆心为
则圆心为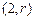 . (8分)
. (8分)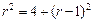 ,
, 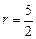 .(10分)
.(10分)圆的方程为
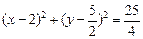 .(11分)
.(11分)(3) 【法一】动圆的方程为:
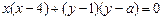 ,(13分) 则
,(13分) 则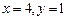 ,(14分)
,(14分)等式恒成立.定点为
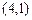 .(16分)
.(16分)【法二】直径所对的圆周角为直角,
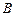 点在直线
点在直线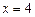 上运动.(13分)
上运动.(13分)过
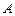 点作
点作 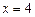 的垂线,垂足为
的垂线,垂足为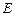 ,则
,则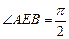 ,(14分)则圆恒过点
,(14分)则圆恒过点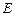
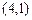 .(16分)
.(16分)
练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
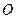 的椭圆
的椭圆 经过点
经过点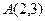 ,且点
,且点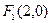 为其右焦点。
为其右焦点。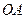 的直线
的直线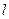 ,使得直线
,使得直线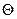 O的切线,P为切点,AC是
O的切线,P为切点,AC是 PAC的内部,点M是BC的中点。
PAC的内部,点M是BC的中点。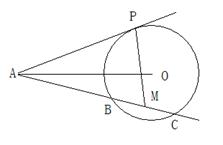
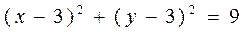 上到直线
上到直线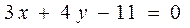 的距离等于1的点有
的距离等于1的点有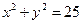 ,过
,过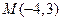 作直线
作直线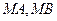 与圆交于点
与圆交于点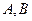 ,且
,且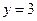 对称,则直线
对称,则直线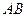 的斜率等于 .
的斜率等于 .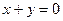 上一点P作圆
上一点P作圆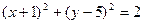 的两条切线
的两条切线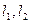 ,A,B为切点,当直线
,A,B为切点,当直线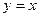 对称时,
对称时,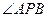 =( )
=( )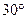
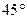
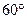
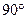
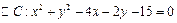 上有四个不同的点到直线
上有四个不同的点到直线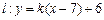 的距离等于
的距离等于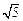 ,则
,则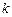 的取值范围是( )
的取值范围是( )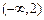
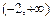
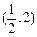
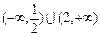
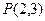 且与圆
且与圆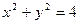 相切的直线方程是 ;
相切的直线方程是 ; 交于P、Q两点,若A恰为PQ的中点,则l的方程为
交于P、Q两点,若A恰为PQ的中点,则l的方程为


