Question

【题目】如图，已知圆C与y轴相切于点T(0,2)，与x轴的正半轴交于两点 (点在点的左侧)，且.

(1)求圆C的方程；(2)过点任作一直线与圆O： 相交于两点，连接，求证： 定值．

Answer 1

【答案】（1） (2)见解析

【解析】试题分析：（1）由题意，得到圆C的方程为2＋(y－2)2＝；（2）直线AB：x＝1＋ty，联立圆O方程，得到韦达定理，求得kAN＋kBN为定值。

试题解析：

(1)因为圆C与y轴相切于点T(0,2)，可设圆心的坐标为(m,2)(m>0)，

则圆C的半径为m，又|MN|＝3，所以m2＝4＋2＝，解得m＝，所以圆C的方程为2＋(y－2)2＝.

(2)由(1)知M(1,0)，N(4,0)，当直线AB的斜率为0时，易知kAN＝kBN＝0，即kAN＋kBN＝0.

当直线AB的斜率不为0时，设直线AB：x＝1＋ty，将x＝1＋ty代入x2＋y2－4＝0，并整理得，(t2＋1)y2＋2ty－3＝0.

设A(x1，y1)，B(x2，y2)，

所以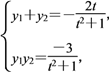

则kAN＋kBN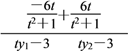＝＋＝＋＝＝＝0.

综上可知，kAN＋kBN为定值．