题目内容
(本小题满分12分)已知函数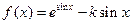 .
.
(Ⅰ)若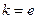 ,试确定函数
,试确定函数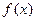 的单调递增区间;
的单调递增区间;
(Ⅱ)若对于任意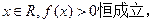 试确定实数
试确定实数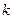 的取值范围;
的取值范围;
(Ⅲ)若函数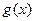 =
=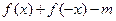 在
在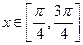 上有两个零点,求实数
上有两个零点,求实数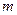 的取值范围.
的取值范围.
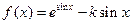 .
. (Ⅰ)若
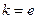 ,试确定函数
,试确定函数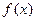 的单调递增区间;
的单调递增区间;(Ⅱ)若对于任意
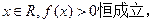 试确定实数
试确定实数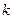 的取值范围;
的取值范围;(Ⅲ)若函数
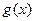 =
=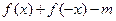 在
在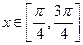 上有两个零点,求实数
上有两个零点,求实数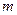 的取值范围.
的取值范围.(Ⅰ)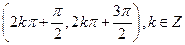 ,(闭区间也正确)
,(闭区间也正确)
(Ⅱ)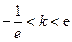 ;
;
(Ⅲ)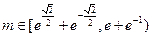 。
。
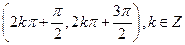 ,(闭区间也正确)
,(闭区间也正确)(Ⅱ)
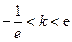 ;
;(Ⅲ)
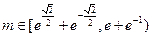 。
。(Ⅰ)由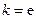 得
得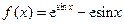 ,则
,则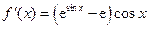 .…1分
.…1分
又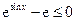 ,故
,故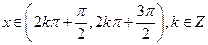 时,
时,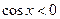 ,
,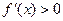 ,
,
所以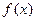 的单调递增区间是
的单调递增区间是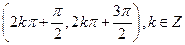 ,注:闭区间也正确………3分
,注:闭区间也正确………3分
(Ⅱ)由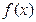 是周期为
是周期为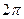 的周期函数.
的周期函数.
所以只需要考虑对任意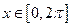 ,
,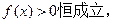
由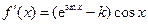
①当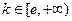 时,类似于第1问,
时,类似于第1问,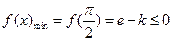 ,不符合题意…4分
,不符合题意…4分
②当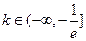 时,有
时,有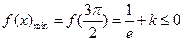 ,不符合题意 ………5分
,不符合题意 ………5分
③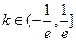 时,也有
时,也有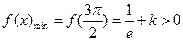 ,符合题意 ……………6分
,符合题意 ……………6分
④当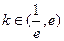 时,令
时,令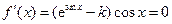 得
得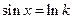 或
或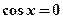
则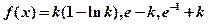 在
在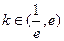 时均大于0,所以
时均大于0,所以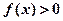 恒成立
恒成立
综上得,实数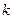 的取值范围是
的取值范围是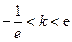 . ……………8分
. ……………8分
(Ⅲ)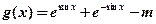 ,
,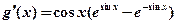
在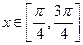 上,
上,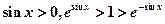 ,
,
所以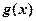 在
在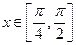 上为增函数,在
上为增函数,在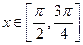 上为减函数,且
上为减函数,且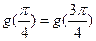
所以当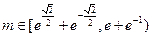 时函数
时函数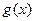 在
在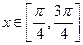 上有两个零点……………12分
上有两个零点……………12分
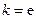 得
得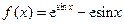 ,则
,则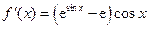 .…1分
.…1分又
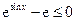 ,故
,故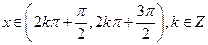 时,
时,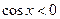 ,
,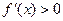 ,
,所以
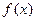 的单调递增区间是
的单调递增区间是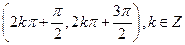 ,注:闭区间也正确………3分
,注:闭区间也正确………3分(Ⅱ)由
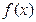 是周期为
是周期为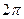 的周期函数.
的周期函数.所以只需要考虑对任意
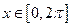 ,
,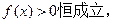
由
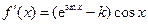
①当
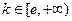 时,类似于第1问,
时,类似于第1问,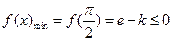 ,不符合题意…4分
,不符合题意…4分②当
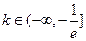 时,有
时,有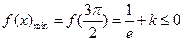 ,不符合题意 ………5分
,不符合题意 ………5分③
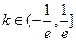 时,也有
时,也有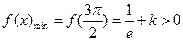 ,符合题意 ……………6分
,符合题意 ……………6分④当
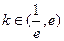 时,令
时,令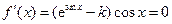 得
得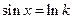 或
或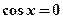
则
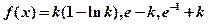 在
在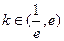 时均大于0,所以
时均大于0,所以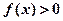 恒成立
恒成立综上得,实数
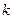 的取值范围是
的取值范围是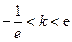 . ……………8分
. ……………8分(Ⅲ)
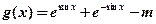 ,
,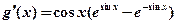
在
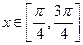 上,
上,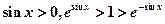 ,
,所以
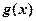 在
在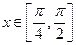 上为增函数,在
上为增函数,在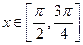 上为减函数,且
上为减函数,且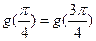
所以当
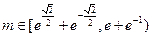 时函数
时函数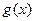 在
在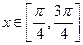 上有两个零点……………12分
上有两个零点……………12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
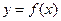 满足:对任意
满足:对任意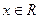 都有
都有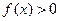 ,且
,且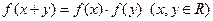
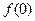 的值;(2)求
的值;(2)求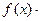
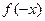 的值;(3)判断函数
的值;(3)判断函数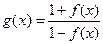 是否具有奇偶性,并证明你的结论。
是否具有奇偶性,并证明你的结论。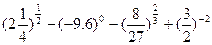 ;
;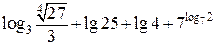 .
.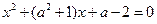 ,有一个根比
,有一个根比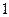 大,另一个根比
大,另一个根比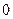 小,
小,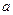 的取值范围是 ( )
的取值范围是 ( )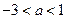
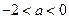
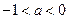
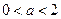
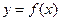 在
在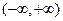 内有定义,对于给定的正数K,定义函数
内有定义,对于给定的正数K,定义函数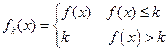 ,取函数
,取函数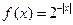 。当
。当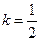 时,函数
时,函数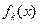 的单调递增区间为 ( )
的单调递增区间为 ( )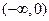
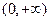
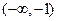
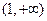
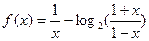 的零点个数为
的零点个数为 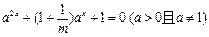 有解,则
有解,则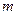 的取值范围是( )
的取值范围是( )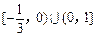
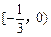
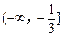
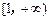
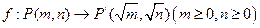 .设点
.设点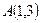 ,
,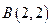 ,点M 是线段AB上一动点,
,点M 是线段AB上一动点,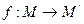 .当点M在线段AB上从点A开始运动到点B结束时,点M的对应点
.当点M在线段AB上从点A开始运动到点B结束时,点M的对应点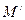 所经过的路线长度为 ( )
所经过的路线长度为 ( )