题目内容
已知f(x)＝log4(2x＋3－x2)，求f(x)的定义域、单调区间和值域；
(1)定义域为{x|－1<x<3}；
(2)单调递增区间为(－1,1]，单调递减区间为[1,3)；
(3)值域为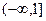
；
(2)单调递增区间为(－1,1]，单调递减区间为[1,3)；
(3)值域为
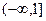；(1)由真数2x＋3－x2>0，解得－1<x<3.
∴定义域是{x|－1<x<3}.
(2)令u＝2x＋3－x2，则u>0，y＝log4u.
由于u＝2x＋3－x2＝－(x－1)2＋4，
考虑到定义域，其增区间是(－1,1]，减区间是[1,3).
又y＝log4u在u∈(0，＋∞)上是增函数，
故该函数的增区间是(－1,1]，减区间是[1,3).
(3)由(2)知，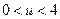
，因为
是增函数，所以其值域为；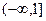
∴定义域是{x|－1<x<3}.
(2)令u＝2x＋3－x2，则u>0，y＝log4u.
由于u＝2x＋3－x2＝－(x－1)2＋4，
考虑到定义域，其增区间是(－1,1]，减区间是[1,3).
又y＝log4u在u∈(0，＋∞)上是增函数，
故该函数的增区间是(－1,1]，减区间是[1,3).
(3)由(2)知，
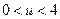，因为是增函数，所以其值域为；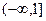
练习册系列答案
相关题目
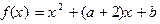满足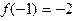
；
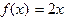有唯一的解，求实数
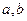的值；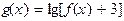
的定义域为R，求实数
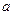的取值范围.
。
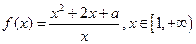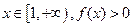恒成立，求实数a的取值范围；
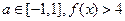恒成立，求实数x的取值范围。
. 
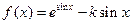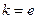，试确定函数
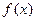的单调递增区间；
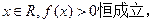试确定实数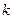
的取值范围；
＝
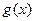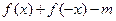在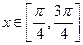
上有两个零点，求实数
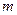的取值范围．
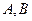两城相距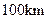
，在两地之间距
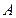城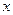
km处建一核电站给
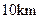。已知供电费用等于供电距离的平方与供电量之积的0.25倍，若
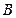城为每月10亿度。
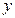表示成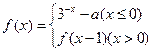
若关于x的方程
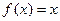有且仅有二个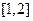
）
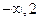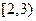
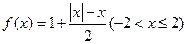
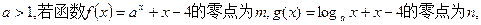
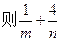的取值范围是（ ）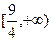
；
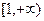
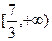
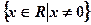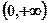上为增函数.