题目内容
10.设有两个命题:①不等式2010x+4>m>2x-x2对一切实数x恒成立;
②函数f(x)=-(7-2m)x是在R上的减函数.
使这两个命题都是真命题的充要条件,用m可表示为1≤m<3.
分析 分别求两个命题成立的等价条件即可.
解答 解:①不等式2010x+4>m>2x-x2对一切实数x恒成立;
∵2010x+4>4,2x-x2=-(x-1)2+1≤1,
∴1≤m≤4
②函数f(x)=-(7-2m)x是在R上的减函数.
则7-2m>1,解得m<3,
故若两个命题都为真命题,则$\left\{\begin{array}{l}{1≤m≤4}\\{m<3}\end{array}\right.$,
解得1≤m<3,
故答案为:1≤m<3
点评 本题主要考查函数恒成立以及充要条件的应用,根据函数的性质是解决本题的关键.

练习册系列答案
相关题目
20.$\frac{{tan{{15}°}}}{{1-{{tan}^2}{{15}°}}}$等于( )
| A. | .$\frac{{\sqrt{3}}}{3}$ | B. | .$\frac{{\sqrt{3}}}{6}$ | C. | .1 | D. | -1 |
1.设全集U={x|x≥0},集合P={1},则∁UP=( )
| A. | [0,1)∪(1,+∞) | B. | (-∞,1) | C. | (-∞,1)∪(1,+∞) | D. | (1,+∞) |
5.已知$a={0.5^{\frac{1}{3}}},b={0.3^{\frac{1}{3}}},c={log_{0.3}}0.2$,则a、b、c的大小关系是( )
| A. | c<b<a | B. | a<b<c | C. | b<a<c | D. | a<c<b |
2.在等差数列{an}中,若a3+a17>0,且a10+a11<0,则使{an}的前n项和Sn有最大值的n为( )
| A. | 12 | B. | 11 | C. | 10 | D. | 9 |
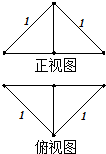 把边长为1的正方形ABCD沿对角线BD折起,形成三棱锥C-ABD,它的正视图与俯视图如图所示,则三棱锥C-ABD的体积为$\frac{\sqrt{2}}{12}$,表面积为1+$\frac{\sqrt{3}}{2}$.
把边长为1的正方形ABCD沿对角线BD折起,形成三棱锥C-ABD,它的正视图与俯视图如图所示,则三棱锥C-ABD的体积为$\frac{\sqrt{2}}{12}$,表面积为1+$\frac{\sqrt{3}}{2}$.