题目内容
15.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,满足:|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=1,($\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-2$\overrightarrow{b}$)=-1(1)求:$\overrightarrow{a}$与$\overrightarrow{b}$的夹角;
(2)求|$\overrightarrow{a}$+$\overrightarrow{b}$|;
(3)若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,求△ABC的面积.
分析 由已知求出向量$\overrightarrow{a}$,$\overrightarrow{b}$的数量积,利用数量积公式求夹角以及模的计算即可.
解答 解:由已知:|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=1,($\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-2$\overrightarrow{b}$)=-1
所以${\overrightarrow{a}}^{2}-2{\overrightarrow{b}}^{2}-\overrightarrow{a}•\overrightarrow{b}$=-1,
所以$\overrightarrow{a}•\overrightarrow{b}=1$,
所以(1)$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的余弦值为$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$,所以$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为45°;
(2)|$\overrightarrow{a}$+$\overrightarrow{b}$|2=${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+2\overrightarrow{a}•\overrightarrow{b}$=2+1+2=5,所以|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{5}$;
(3)若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则△ABC的面积$\frac{1}{2}×|\overrightarrow{a}||\overrightarrow{b}|sinC$=$\frac{1}{2}×\sqrt{2}×1×\frac{\sqrt{2}}{2}$=1.
点评 本题考查了平面向量的数量积公式的运用、模的求法以及三角形面积公式的运用;关键是正确求出$\overrightarrow{a}$,$\overrightarrow{b}$,的夹角.

 天天练口算系列答案
天天练口算系列答案| A. | {x|x>$\frac{1}{2}$或x<$\frac{1}{4}$} | B. | {x|x<$\frac{1}{4}$} | C. | {x|x>$\frac{1}{2}$} | D. | {x|$\frac{1}{2}$<x<$\frac{1}{4}$} |
| A. | 若m∥β,β⊥α则m⊥α | B. | 若m⊥n,n⊥β,β⊥α,则m⊥α | ||
| C. | 若m⊥α,m⊥n则n∥α | D. | 若m⊥α,n?α,则m⊥n |
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{3}$ | D. | $\frac{23}{27}$ |
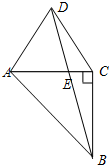 如图所示,△ACD是边长为1的等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于点E.则线段AE的长为$\sqrt{3}$-1.
如图所示,△ACD是边长为1的等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于点E.则线段AE的长为$\sqrt{3}$-1.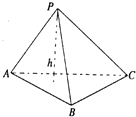 在Rt△ABC中,两直角边分别为a,b,设h为斜边上的高,则$\frac{1}{h^2}$=$\frac{1}{a^2}$+$\frac{1}{b^2}$,类比此性质,如图,在四面体P-ABC 中,若PA,PB,PC两两垂直,且长度分别为a,b,c,设棱锥底面ABC上的高为h,则得到的正确结论为$\frac{1}{h^2}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}$.
在Rt△ABC中,两直角边分别为a,b,设h为斜边上的高,则$\frac{1}{h^2}$=$\frac{1}{a^2}$+$\frac{1}{b^2}$,类比此性质,如图,在四面体P-ABC 中,若PA,PB,PC两两垂直,且长度分别为a,b,c,设棱锥底面ABC上的高为h,则得到的正确结论为$\frac{1}{h^2}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}$.