题目内容
（2013•未央区三模）（坐标系与参数方程）在极坐标系中，曲线ρ=4cos(θ-
)与直线ρsin(θ+
)=1的两个交点之间的距离为
| π |
| 3 |
| π |
| 6 |
2
| 3 |
2
．| 3 |
分析：根据极坐标公式进行化简就可求出曲线与直线的直角坐标方程，再利用直角坐标方程的形式，先求出圆心（0，0）到直线的距离，最后结合点到直线的距离公式弦的长度．
解答：解：把曲线方程ρ=4cos(θ-
)化为直角坐标方程为：x2+y2=9，
把直线方程ρsin(θ+
)=1转化为直角坐标方程为x+
y-2=0，
圆心到直线的距离为：d=
=1，
所以弦长为2
=2
，
即两个交点之间的距离为2
．
故答案为：2
．
| π |
| 3 |
把直线方程ρsin(θ+
| π |
| 6 |
| 3 |
圆心到直线的距离为：d=
|1+
| ||||
| 2 |
所以弦长为2
| r2-d2 |
| 3 |
即两个交点之间的距离为2
| 3 |
故答案为：2
| 3 |
点评：本题主要考查了简单曲线的极坐标方程，以及利用圆的几何性质计算圆心到直线的距等基本方法，属于基础题．
练习册系列答案
初中学业考试导与练系列答案
相关题目
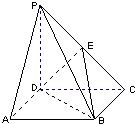（2013•未央区三模）如图，四棱锥P-ABCD的底面ABCD是正方形，棱PD⊥底面ABCD，PD=DC，E是PC的中点．
（2013•未央区三模）某三棱锥的三视图如图所示，该三棱锥的体积是为（ ）