题目内容
(2013•未央区三模)在数列{an}中,a1=
,且对任意的n∈N+都有an+1=
.
(Ⅰ)求证:{
-1}是等比数列;
(Ⅱ)若对于任意n∈N+都有an+1<pan,求实数P的取值范围.
| 2 |
| 3 |
| 2an |
| an+1 |
(Ⅰ)求证:{
| 1 |
| an |
(Ⅱ)若对于任意n∈N+都有an+1<pan,求实数P的取值范围.
分析:(Ⅰ)直接利用an+1=
可得
-1=
-1=
=
(
-1);再求出首项不为0即可证:{
-1}是等比数列;
(Ⅱ)先利用(Ⅰ)的结论求出数列{an}的通项,代入an+1<pan把其整理为p>1+
,再利用函数的单调性求出不等式右边的取值范围即可得出实数P的取值范围.
| 2an |
| an+1 |
| 1 |
| an+1 |
| an+1 |
| 2an |
| 1-an |
| 2an |
| 1 |
| 2 |
| 1 |
| an |
| 1 |
| an |
(Ⅱ)先利用(Ⅰ)的结论求出数列{an}的通项,代入an+1<pan把其整理为p>1+
| 1 |
| 2n+1+1 |
解答:解:
(Ⅰ)证明:由an+1=
,得
-1=
-1=
=
(
-1).
又由a1=
,得
-1=
≠0.
∴{
-1}是以
-1=
为首项,以
为公比的等比数列.
(Ⅱ)由(Ⅰ),可得
-1=
×(
)n-1=
.
即an=
,an+1=
.
∵an+1<pan(n∈N+),
∴p>
=
•
=
=1+
显然,当n=1时,1+
值最大,且最大值为
.
∴实数p的取值范围为p>
.
(Ⅰ)证明:由an+1=
| 2an |
| an+1 |
| 1 |
| an+1 |
| an+1 |
| 2an |
| 1-an |
| 2an |
| 1 |
| 2 |
| 1 |
| an |
又由a1=
| 2 |
| 3 |
| 1 |
| a1 |
| 1 |
| 2 |
∴{
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)由(Ⅰ),可得
| 1 |
| an |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2n |
即an=
| 2n |
| 2n+1 |
| 2n+1 |
| 2n+1+1 |
∵an+1<pan(n∈N+),
∴p>
| an+1 |
| an |
| 2n+1 |
| 2n+1+1 |
| 2n+1 |
| 2n |
| 2n+1+2 |
| 2n+1+1 |
| 1 |
| 2n+1+1 |
显然,当n=1时,1+
| 1 |
| 2n+1+1 |
| 6 |
| 5 |
∴实数p的取值范围为p>
| 6 |
| 5 |
点评:本题主要考查数列递推关系式的应用以及等比数列的证明和数列与函数的综合问题,是对知识点的综合考查,属于中档题目.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
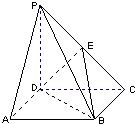 (2013•未央区三模)如图,四棱锥P-ABCD的底面ABCD是正方形,棱PD⊥底面ABCD,PD=DC,E是PC的中点.
(2013•未央区三模)如图,四棱锥P-ABCD的底面ABCD是正方形,棱PD⊥底面ABCD,PD=DC,E是PC的中点. (2013•未央区三模)某三棱锥的三视图如图所示,该三棱锥的体积是为( )
(2013•未央区三模)某三棱锥的三视图如图所示,该三棱锥的体积是为( )