题目内容
【题目】如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.
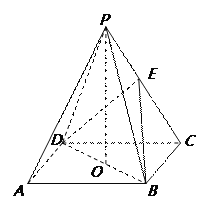
.求证:(Ⅰ)PA∥平面BDE;(Ⅱ)平面PAC⊥平面BDE;(III)若PB与底面所成的角为600, AB=2a,求三棱锥E-BCD的体积.
【答案】(1)见解析;(2)![]() .
.
【解析】【试题分析】(1)先借助题设证明OE∥AP,再运用线面平行的判定定理推证PA∥平面BDE;(2)先运用线面垂直的判定定理证明BD⊥平面PAC,再依据面面垂直的判定定理证明平面PAC⊥平面BDE;(3)题借助题设中线面角的定义求出三棱锥的高,再运用三棱锥的体积公式求解:
证明:(I)∵O是AC的中点,E是PC的中点,
∴OE∥AP,
又∵OE平面BDE,PA平面BDE.
∴PA∥平面BDE.
(II)∵PO⊥底面ABCD,PO⊥BD,
又∵AC⊥BD,且AC∩PO=O
∴BD⊥平面PAC,
而BD平面BDE,
∴平面PAC⊥平面BDE.
(III)∵ PB与底面所成的角为600,且PO⊥底面ABCD,∴∠PBO=600,
∵ AB=2a, ∴BO=![]() a PO=
a PO=![]() a,
a,
∴E到面BCD的距离= ![]() a
a
∴三棱锥E-BCD的体积V=![]() .
.

 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案【题目】目前,学案导学模式已经成为教学中不可或缺的一部分,为了了解学案的合理使用是否对学生的期末复习有着重要的影响,我校随机抽取100名学生,对学习成绩和学案使用程度进行了调查,统计数据如表所示:
善于使用学案 | 不善于使用学案 | 总计 | |
学习成绩优秀 | 40 | ||
学习成绩一般 | 30 | ||
总计 | 100 |
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
已知随机抽查这100名学生中的一名学生,抽到善于使用学案的学生概率是0.6.
(1)请将上表补充完整(不用写计算过程);
(2)试运用独立性检验的思想方法分析:有多大的把握认为学生的学习成绩与对待学案的使用态度有关?
(3)若从学习成绩优秀的同学中随机抽取10人继续调查,采用何种方法较为合理,试说明理由.