Question

【题目】如图，在△ABC中，∠C=60°，D是BC上一点，AB=31，BD=20，AD=21．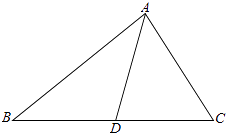
（1）求cos∠B的值；
（2）求sin∠BAC的值和边BC的长．

Answer 1

【答案】
（1）在△ABC中，cosB= = =
（2）0°＜B＜180°，由（1）可得：sinB= = ，

∴sin∠BAC=sin[180°﹣（B+60°）]=sin（B+60°）=sinBcos60°+cosBsin60°= + = ．

在△ABC中，由正弦定理可得： = ，

∴BC= = =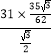35

【解析】（1）利用余弦定理可得cosB= ．（2）0°＜B＜180°，由（1）可得：sinB= = ，可得sin∠BAC=sin[180°﹣（B+60°）]=sin（B+60°）．在△ABC中，由正弦定理可得： = ，即可得出．