题目内容
18. 如图,圆O中AB=4为直径,直线CE与圆O相切于点C,AD⊥CE于点D,若AD=1,∠ACD=θ,则cosθ=$\frac{\sqrt{3}}{2}$.
如图,圆O中AB=4为直径,直线CE与圆O相切于点C,AD⊥CE于点D,若AD=1,∠ACD=θ,则cosθ=$\frac{\sqrt{3}}{2}$.
分析 利用圆的性质、切线的性质、三角形相似的判定与性质、三角函数的定义即可得出.
解答 解:根据弦切角定理得,△BCA与△CDA相似,所以$\frac{AC}{AB}=\frac{AD}{AC}$,
所以AC=2.
在直角三角形ACD中可得CD=$\sqrt{3}$,
所以cosθ=$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$.
点评 熟练掌握圆的性质、切线的性质、三角形相似的判定与性质、三角函数的定义是解题的关键.

练习册系列答案
相关题目
8.若曲线y=$\frac{x+1}{x-1}$在点(3,2)处的切线与直线ax+y+1=0平行,则a=( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |
9.已知向量$\overrightarrow{a}$=(x,1),$\overrightarrow{b}$=(4,x),$\overrightarrow{a}$∥$\overrightarrow{b}$,则实数x的值是( )
| A. | 0 | B. | ±2 | C. | 2 | D. | -2 |
13.图1为某村1000户村民月用电量(单位:度)的频率分布直方图,记月用电量在[50,100)的用户数为A1,用电量在[100,150)的用户数为A2,…,以此类推,用电量在[300,350]的用户数为A6,图2是统计图1中村民月用电量在一定范围内的用户数的一个算法流程图.根据图1提供的信息,则图2中输出的s值为( )
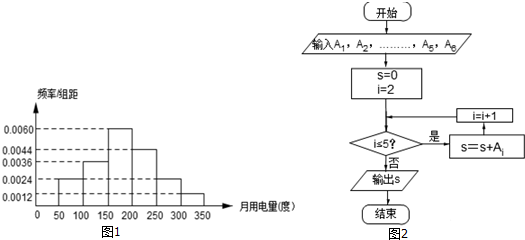

| A. | 820 | B. | 720 | C. | 620 | D. | 520 |
7.在平面直角坐标系xOy中,双曲线中心在原点,焦点在y轴上,离心率为$\sqrt{5}$,则其渐进线方程为( )
| A. | y=$\frac{1}{2}$x | B. | y=±$\frac{1}{2}$x | C. | y=-$\frac{1}{2}$x | D. | y=±2x |
8.若以A、B为焦点的双曲线经过点C,且|AB|=|AC|,cos∠ABC=$\frac{1}{3}$,则该双曲线的离心率为( )
| A. | $\frac{3}{2}$ | B. | 2 | C. | 3 | D. | $\frac{5}{2}$ |