题目内容
【题目】随着互联网的发展,移动支付(又称手机支付)越来越普通,某学校兴趣小组为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有![]() 个人.把这
个人.把这![]() 个人按照年龄分成5组:第1组
个人按照年龄分成5组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,然后绘制成如图所示的频率分布直方图.其中,第一组的频数为20.
,然后绘制成如图所示的频率分布直方图.其中,第一组的频数为20.
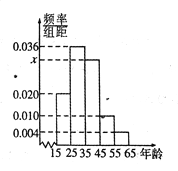
(1)求![]() 和
和![]() 的值,并根据频率分布直方图估计这组数据的众数;
的值,并根据频率分布直方图估计这组数据的众数;
(2)从第1,3,4组中用分层抽样的方法抽取6人,求第1,3,4组抽取的人数;
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
【答案】(1)![]() ,
,![]() ,30;(2)第1组2人,第2组3人,第3组1人;(3)
,30;(2)第1组2人,第2组3人,第3组1人;(3)![]() .
.
【解析】试题分析:(1)直接利用频率分布直方图,结合累积频率为1,频数=频率×样本容量,可分别求出![]() 和
和![]() 的值,最高点的中点横坐标即为众数;
的值,最高点的中点横坐标即为众数;
(2)直接利用抽样比即可求第1,2,3组每组各抽取人数.
(3)列出(2)抽取的6人中随机抽取2人是所有情况,求出这2人来自同一个组的数目,即可求解概率.
试题解析:
(1)由题意可知,![]() ,
,
由![]() ,
,
解得![]() ,
,
由频率分布直方图可估计这组数据的众数为30;
(2)第1,3,4组频率之比为0.020:0.030:0.010=2:3:1
则从第1组抽取的人数为![]() ,
,
从第3组抽取的人数为![]() ,
,
从第4组抽取的人数为![]() ;
;
(3)设第1组抽取的2人为![]() ,第3组抽取的3人为
,第3组抽取的3人为![]() ,第4组抽取的1人为
,第4组抽取的1人为![]() ,则从这6人中随机抽取2人有如下种情形:
,则从这6人中随机抽取2人有如下种情形:![]() ,
,
![]() ,共有15个基本事件.
,共有15个基本事件.
其中符合“抽取的2人来自同一个组”的基本事件有![]() 共4个基本事件,
共4个基本事件,
所以抽取的2人来自同一个组的概率![]() .
.

【题目】利用独立性检验的方法调查大学生的性别与爱好某项运动是否有关,通过随机询问110名不同的大学生是否爱好某项运动,利用![]() 列联表,由计算可得
列联表,由计算可得![]()
P(K2>k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参照附表,得到的正确结论是( )
A.有99.5%以上的把握认为“爱好该项运动与性别无关”
B.有99.5%以上的把握认为“爱好该项运动与性别有关”
C.在犯错误的概率不超过0.05%的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过0.05%的前提下,认为“爱好该项运动与性别无关”