题目内容
【题目】关于![]() 的方程
的方程![]() 恰有3个实数根
恰有3个实数根![]() ,
,![]() ,
,![]() ,则
,则![]() __________.
__________.
【答案】2
【解析】
令f(x)=x2+arcsin(cosx)+a,判断f(x)的奇偶性,由题意可得f(0)=0,求得a,再由反三角函数的定义和性质,化简函数,求得f(x)=0的解,即可得到所求和.
令f(x)=x2+arcsin(cosx)+a,
可得f(﹣x)=(﹣x)2+arcsin(cos(﹣x))+a=f(x),
则f(x)为偶函数,
∵f(x)=0有三个实数根,
∴f(0)=0,即0![]() a=0,故有a
a=0,故有a![]() ,
,
关于x的方程即x2+arcsin(cosx)![]() 0,
0,
可设![]() =0,
=0,
且![]() 2+arcsin(cos
2+arcsin(cos![]() )
)![]() 0,
0,
![]() 2+arcsin(cos
2+arcsin(cos![]() )
)![]() 0,
0,
![]() =﹣
=﹣![]() ,
,
由y=x2和y![]() arcsin(cosx),
arcsin(cosx),
当x>0,且0<x<π时,y![]() arcsin(cosx)
arcsin(cosx)![]() arcsin(sin(
arcsin(sin(![]() x))
x))
![]() (
(![]() x))=x,
x))=x,
则﹣π<x<0时,y![]() arcsin(cosx)=﹣x,
arcsin(cosx)=﹣x,
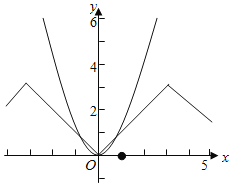
由y=x2和y![]() arcsin(cosx)的图象可得:
arcsin(cosx)的图象可得:
它们有三个交点,且为(0,0),(﹣1,1),(1,1),
则![]() 2+
2+![]() 2+
2+![]() 2=0+1+1=2.
2=0+1+1=2.
故答案为:2.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目