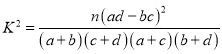题目内容
【题目】己知函数![]() ,若关于
,若关于![]() 的方程
的方程![]() 有8个不等的实数根,则
有8个不等的实数根,则![]() 的取值范围是_________.
的取值范围是_________.
【答案】![]()
【解析】
由f2(x)﹣bf(x)+c=0有8个不同实数解,令f(x)=k,则关于k的方程有2个不同的解,根据题意作出f(x)的简图,由图可知,只有满足条件的k在开区间(0,1)时符合题意.再根据一元二次方程根的分布列出不等关系,结合线性规划的知识求解得出答案.
根据题意作出f(x)的简图:
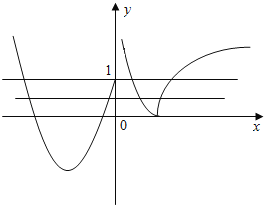
由图象可得当f(x)∈(0,1]时,有四个不同的x与f(x)对应.再结合题中“方程f2(x)﹣bf(x)+c=0有8个不同实数解”,
可以分解为形如关于k的方程k2﹣bk+c=0有两个不同的实数根K1、K2,且K1和K2均为大于0且小于等于1的实数.
列式如下: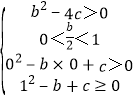 ,化简得
,化简得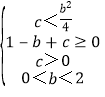 ,
,
此不等式组表示的区域如图:
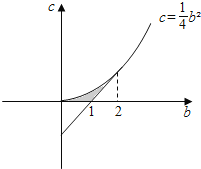
令z=b+c,则z=b+c在(2,1)处z=3,在(0,0)处z=0,
所以b+c的取值范围为(0,3),
故答案为(0,3).

 阅读快车系列答案
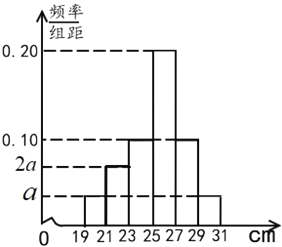
阅读快车系列答案【题目】某市为了了解民众对开展创建文明城市工作以来的满意度,随机调查了40名群众,并将他们随机分成![]() ,
,![]() 两组,每组20人,
两组,每组20人,![]() 组群众给第一阶段的创文工作评分,
组群众给第一阶段的创文工作评分,![]() 组群众给第二阶段的创文工作评分,根据两组群众的评分绘制了如图所示的茎叶图.
组群众给第二阶段的创文工作评分,根据两组群众的评分绘制了如图所示的茎叶图.
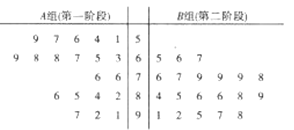
(Ⅰ)根据茎叶图比较群众对两个阶段的创文工作满意度评分的平均值和集中程度(不要求计算出具体值,给出结论即可);
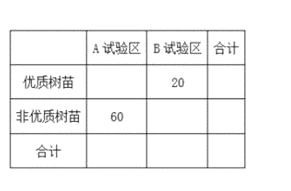
(Ⅱ)完成下面的列联表,并通过计算判断是否有![]() 的把握认为民众对两个阶段创文工作的满意度存在差异?
的把握认为民众对两个阶段创文工作的满意度存在差异?
低于70分 | 不低于70分 | 合计 | |
第一阶段 | |||
第二阶段 | |||
合计 |
参考公式:![]() ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】(2014·长春模拟)对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表:
甲 | 27 | 38 | 30 | 37 | 35 | 31 |
乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图.
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、方差,并判断选谁参加比赛更合适?