题目内容
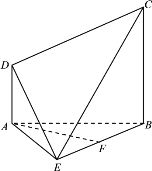
【题目】如图,在多面体![]() 中,
中,![]() 为等边三角形,
为等边三角形,![]()
![]() ,
,![]() 点
点![]() 为边
为边![]() 的中点.
的中点.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)见解析; (Ⅱ)见解析; (Ⅲ)![]() .
.
【解析】
(I)取![]() 中点
中点![]() ,连结
,连结![]() ,利用三角形中位线定理可证明
,利用三角形中位线定理可证明![]() 是平行四边形,可得
是平行四边形,可得![]() ,由线面平行的判定定理可得结果;(Ⅱ)先证明
,由线面平行的判定定理可得结果;(Ⅱ)先证明![]() ,
,![]() ,可得
,可得![]() 平面
平面![]() ,从而可得
,从而可得![]() 平面
平面![]() ,由面面垂直的判定定理可得结果;(Ⅲ)取
,由面面垂直的判定定理可得结果;(Ⅲ)取![]() 中点
中点![]() ,连结
,连结![]() ,直线
,直线![]() 与平面
与平面![]() 所成角等于直线
所成角等于直线![]() 与平面
与平面![]() 所成角,
所成角,
过![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,![]() 为直线
为直线![]() 与平面
与平面![]() 所成角,利用直角三角形的性质可得结果.
所成角,利用直角三角形的性质可得结果.
(I)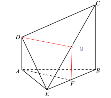
取![]() 中点
中点![]() ,连结
,连结![]()
![]() ,
,
![]() 是平行四边形,
是平行四边形,
![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() .
.
(II) ![]() ,
,
又![]()
![]() 平面
平面![]()
![]() 平面
平面![]()
![]() ,
,
又![]() 为等边三角形,
为等边三角形,![]() 为边
为边![]() 的中点,
的中点,![]()
![]() 平面
平面![]()
由(I)可知,![]()
![]() 平面
平面![]() ,
,
![]() 平面
平面![]()
![]() 平面
平面![]() 平面
平面![]() 。
。
(III) 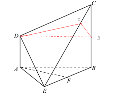
取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]()
所以直线![]() 与平面
与平面![]() 所成角即为直线
所成角即为直线![]() 与平面
与平面![]() 所成角,
所成角,
过![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.
![]() 平面
平面![]() 平面
平面![]()
![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() .
.
![]() 为斜线
为斜线![]() 在面
在面![]() 内的射影,
内的射影,![]() 为直线
为直线![]() 与平面
与平面![]() 所成角,
所成角,
在![]() 中,
中,![]()
![]()
![]() 直线
直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案【题目】某种商品在![]() 天内每件的销售价格
天内每件的销售价格![]() (元)与时间
(元)与时间![]() (
(![]() )(天)的函数关系满足函数
)(天)的函数关系满足函数 ,该商品在
,该商品在![]() 天内日销售量
天内日销售量![]() (件)与时间
(件)与时间![]() (
(![]() )(天)之间满足一次函数关系如下表:
)(天)之间满足一次函数关系如下表:
第 |
|
|
|
|
|
|
|
|
|
(1)根据表中提供的数据,确定日销售量![]() 与时间
与时间![]() 的一次函数关系式;
的一次函数关系式;
(2)求该商品的日销售金额的最大值并指出日销售金额最大的一天是![]() 天中的第几天,(日销售金额
天中的第几天,(日销售金额![]() 每件的销售价格
每件的销售价格![]() 日销售量)
日销售量)
【题目】为了研究家用轿车在高速公路上的车速情况,交通部门随机对50名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在30名男性驾驶员中,平均车速超过![]() 的有20人,不超过
的有20人,不超过![]() 的有10人.在20名女性驾驶员中,平均车速超过
的有10人.在20名女性驾驶员中,平均车速超过![]() 的有5人,不超过
的有5人,不超过![]() 的有15人.
的有15人.
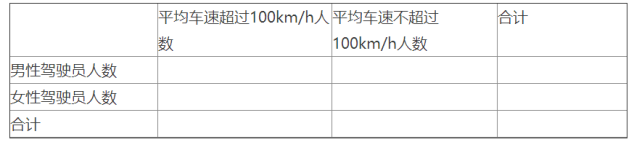
(1)完成下面的列联表,并判断是否有99.5%的把握认为平均车速超过的人与性别有关;
(2)以上述数据样本来估计总体,现从高速公路上行驶的大量家用轿车中随机抽取3辆,记这3辆车中驾驶员为女性且车速不超过![]() 的车辆数为
的车辆数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的数学期望.
的数学期望.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如图: 
(1)记事件A为:“从这批小龙虾中任取一只,重量不超过35g的小龙虾”,求P(A)的估计值;
(2)若购进这批小龙虾100千克,试估计这批小龙虾的数量;
(3)为适应市场需求,了解这批小龙虾的口感,该经销商将这40只小龙虾分成三个等级,如下表:
等级 | 一等品 | 二等品 | 三等品 |
重量(g) | [5,25) | [25,45) | [45,55] |
按分层抽样抽取10只,再随机抽取3只品尝,记X为抽到二等品的数量,求抽到二级品的期望.