题目内容
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,PA=AD=2,点M、N分别在棱PD、PC的中点.
(1)求证:PD⊥平面AMN;
(2)求三棱锥P-AMN的体积;
(3)求二面角P-AN-M的大小.
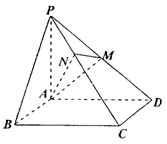
(1)求证:PD⊥平面AMN;
(2)求三棱锥P-AMN的体积;
(3)求二面角P-AN-M的大小.

(1)∵ABCD是正方形,
∴CD⊥AD
∵PA⊥底面ABCD,
∴AD是PD在平面ABCD内的射影,
∴CD⊥PD
在△PCD中,M、N分别为PD、PC的中点,则MN∥CD,
∴MN⊥PD
∵在△PAD中,PA=AD=2,M为PD的点,
∴AM⊥PD,
∵AM∩MN=M,AM?平面AMN,MN?平面AMN
∴PD⊥平面AMN
(2)∵CD⊥AD,CD⊥PD,
∴CD⊥平面PAD.
∵MN∥CD,
∴MN⊥平面PAD
又∵AM?平面PAD
∴MN⊥AM,即∠AMN=90°,
∵在Rt△PAD中,PA=AD=2,M为PD的中点,
∴AM=PM=
.
又∵MN=
CD=1,
∴S△AMN=
AM•MN=
.
∵PM⊥平面AMN,
∴PM为三棱锥P-AMN的高,
∴V三棱锥P-AMN=
S△AMN•PM=
.
(3)作MH⊥AN于H,连接PH,
∵PM⊥平面AMN,
∴PH⊥AN,
∴∠PHM为二面角P-AN-M的平面角
∵PM⊥平面AMN,
∴PM⊥MH.
在Rt△AMN中,MH=
=
,
∴在Rt△PMH中,tan∠PHM=
=
=
,
∴∠PHM=60°则二面角P-AN-M的大小为60°.

∴CD⊥AD
∵PA⊥底面ABCD,
∴AD是PD在平面ABCD内的射影,
∴CD⊥PD
在△PCD中,M、N分别为PD、PC的中点,则MN∥CD,
∴MN⊥PD
∵在△PAD中,PA=AD=2,M为PD的点,
∴AM⊥PD,
∵AM∩MN=M,AM?平面AMN,MN?平面AMN
∴PD⊥平面AMN
(2)∵CD⊥AD,CD⊥PD,
∴CD⊥平面PAD.
∵MN∥CD,
∴MN⊥平面PAD
又∵AM?平面PAD
∴MN⊥AM,即∠AMN=90°,
∵在Rt△PAD中,PA=AD=2,M为PD的中点,
∴AM=PM=
| 2 |
又∵MN=
| 1 |
| 2 |
∴S△AMN=
| 1 |
| 2 |
| ||
| 2 |
∵PM⊥平面AMN,
∴PM为三棱锥P-AMN的高,
∴V三棱锥P-AMN=
| 1 |
| 3 |
| 1 |
| 3 |
(3)作MH⊥AN于H,连接PH,
∵PM⊥平面AMN,
∴PH⊥AN,
∴∠PHM为二面角P-AN-M的平面角
∵PM⊥平面AMN,
∴PM⊥MH.
在Rt△AMN中,MH=
| AM•MN |
| AN |
| ||
|
∴在Rt△PMH中,tan∠PHM=
| PM |
| MH |
| ||||||
|
| 3 |
∴∠PHM=60°则二面角P-AN-M的大小为60°.


练习册系列答案
相关题目