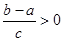题目内容
数列{an}满足a1>1,an+1-1=an(an-1),(n∈N+),且
+
+…+
=2,则a2013-4a1的最小值为______.
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2012 |
a1>1,由an+1-1=an(an-1),(n∈N+)知,对所有n,an>1,
等式两边取倒数,得
=
=
-
,得,
=
-
,
则
+
+…+
=
-
=2
整理可得,a2013=
,
a2013-4a1=2(3-2a1)+
-
≥2
-
=-
.
则a2013-4a1的最小值为 -
.
故答案为:-
.
等式两边取倒数,得
| 1 |
| an+1-1 |
| 1 |
| an(an-1) |
| 1 |
| an-1 |
| 1 |
| an |
| 1 |
| an |
| 1 |
| an-1 |
| 1 |
| an+1-1 |
则
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2012 |
| 1 |
| a1 |
| 1 |
| a2013 |
整理可得,a2013=
| 2-a1 |
| 3-2a1 |
a2013-4a1=2(3-2a1)+
| 1 |
| 2(3-2a1) |
| 11 |
| 2 |
(3-2a1)
|
| 11 |
| 2 |
| 7 |
| 2 |
则a2013-4a1的最小值为 -
| 7 |
| 2 |
故答案为:-
| 7 |
| 2 |

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 的前
的前 项和
项和 ,则此数列的通项公式为 .
,则此数列的通项公式为 . 满足
满足 且
且 ,则下列选项中不一定能成立的是( )
,则下列选项中不一定能成立的是( )