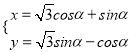题目内容
【题目】以直角坐标系原点O为极点,x轴的正半轴为极轴.已知点P的直角坐标为![]() ,点M的极坐标为
,点M的极坐标为![]() ,若直线l过点P,且倾斜角为
,若直线l过点P,且倾斜角为![]() ,圆C以M点为圆心,4为半径.
,圆C以M点为圆心,4为半径.
![]() 求直线l和圆C的极坐标方程;
求直线l和圆C的极坐标方程;
![]() 直线l与x轴y轴分别交于A,B两点,Q为圆C上一动点,求
直线l与x轴y轴分别交于A,B两点,Q为圆C上一动点,求![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() .
.![]() .(2)
.(2)![]() .
.
【解析】
![]() 先求出直线l的直角坐标方程,由此能求出直线l的极坐标方程,先求出圆C的直角坐标方程,由此能求出圆C的极坐标方程.
先求出直线l的直角坐标方程,由此能求出直线l的极坐标方程,先求出圆C的直角坐标方程,由此能求出圆C的极坐标方程.
![]() 直线l与x轴交与
直线l与x轴交与![]() ,直线l与y轴交于
,直线l与y轴交于![]() ,
,![]() ,圆心到直线l的距离为
,圆心到直线l的距离为![]() ,由此能求出
,由此能求出![]() 面积的最小值.
面积的最小值.
解:![]() 点P的直角坐标为
点P的直角坐标为![]() ,直线l过点P,且倾斜角为
,直线l过点P,且倾斜角为![]() ,
,
![]() 直线l的直角坐标方程为
直线l的直角坐标方程为![]() ,即
,即![]() ,
,
![]() 直线l的极坐标方程为:
直线l的极坐标方程为:![]() .
.
![]() 点M的极坐标为
点M的极坐标为![]() ,
,![]() 的直角坐标为
的直角坐标为![]() ,
,
![]() 圆C以M点为圆心,4为半径,
圆C以M点为圆心,4为半径,
![]() 圆C的直角坐标方程为
圆C的直角坐标方程为![]() ,即
,即![]() ,
,
![]() 圆C的极坐标方程为:
圆C的极坐标方程为:![]() ,即
,即![]() .
.
![]() 直线l与x轴交与
直线l与x轴交与![]() ,直线l与y轴交于
,直线l与y轴交于![]() ,
,![]() ,
,
圆心到直线l的距离为![]() ,
,
![]() 面积的最小值为:
面积的最小值为:
![]() .
.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目