题目内容
【题目】关于函数的对称性有如下结论:对于给定的函数![]() ,如果对于任意的
,如果对于任意的![]() 都有
都有![]() 成立
成立![]() 为常数),则函数
为常数),则函数![]() 关于点
关于点![]() 对称.
对称.
(1)用题设中的结论证明:函数![]() 关于点
关于点![]() ;
;
(2)若函数![]() 既关于点
既关于点![]() 对称,又关于点
对称,又关于点![]() 对称,且当
对称,且当![]() 时,
时,![]() ,求:①
,求:①![]() 的值;
的值;
②当![]() 时,
时,![]() 的表达式.
的表达式.
【答案】(1)证明见解析;(2)①![]() ;②
;②![]() .
.
【解析】
(1)根据题设中的结论证明即可;
(2)由题意可得![]() ,①代值计算即可;②由
,①代值计算即可;②由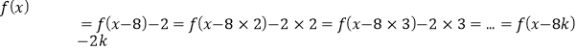 ,然后代值计算即可.
,然后代值计算即可.
(1)f(x)=![]() 的定义域为{x|x≠3},对任意x≠3有f(3﹣x)+f(3﹣x)=(﹣2﹣
的定义域为{x|x≠3},对任意x≠3有f(3﹣x)+f(3﹣x)=(﹣2﹣![]() )+(﹣2﹣
)+(﹣2﹣![]() )=﹣4,
)=﹣4,
∴函数f(x)=![]() 关于点(3,﹣2)对称;
关于点(3,﹣2)对称;
(2)函数f(x)关于点(2,0)对称,
∴f(2+x)+f(2﹣x)=0,
即f(x)+f(4﹣x)=0,
又关于点(﹣2,1)对称,
∴f(﹣2+x)+f(﹣2﹣x)=2,
即f(x)+f(﹣4﹣x)=2,
∴f(﹣4﹣x)=2+f(4﹣x),
即f(x+8)=f(x)﹣2,
①f(﹣5)=f(3)+2=23+3×3+2=19,
②x∈(8k﹣2,8k+2),x﹣8k∈(﹣2,2),4﹣(x﹣8k)∈(2,6),
∴f(x)=f(x﹣8)﹣2=f(x﹣8×2)﹣2×2=f(x﹣8×3)﹣2×3=…=f(x﹣8k)﹣2k,
又由f(t)=﹣f(4﹣t),
∴f(x)=f(x﹣8k)﹣2k=﹣f[4﹣(x﹣8k)]﹣2k=﹣[24﹣(x﹣8k)+3(4﹣(x﹣8k))]﹣2k,
∴即当x∈(8k﹣2,8k+2),k∈Z时,f(x)=﹣24﹣x+8k+3x﹣26k﹣12.

 阅读快车系列答案
阅读快车系列答案【题目】某校夏令营有3名男同学![]() 和3名女同学
和3名女同学![]() ,其年级情况如下表,现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同).
,其年级情况如下表,现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同).
一年级 | 二年级 | 三年级 | |
男同学 |
|
|
|
女同学 |
|
|
|
(1)用表中字母列举出所有可能的结果;
(2)设![]() 为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件
为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件![]() 发生的概率.
发生的概率.
