题目内容
【题目】已知直线l过定点P(1,1),且倾斜角为 ![]() ,以坐标原点为极点,x轴的正半轴为极轴的坐标系中,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴的坐标系中,曲线C的极坐标方程为 ![]() .
.
(1)求曲线C的直角坐标方程与直线l的参数方程;
(2)若直线l与曲线C相交于不同的两点A,B,求|AB|及|PA||PB|的值.
【答案】
(1)解:∵曲线C的极坐标方程为 ![]() ,
,
∴ρ2=2ρcosθ+3,
将ρ2=x2+y2,ρcosθ=x代入,得x2+y2=2x+3,即x2+y2﹣2x﹣3=0.
∵直线l过定点P(1,1),且倾斜角为 ![]() ,
,
则直线l的参数方程为 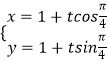 ,即
,即 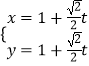 (t为参数)
(t为参数)
(2)解:将直线l的参数方程代入x2+y2﹣2x﹣3=0,得 ![]() ,
,
设方程两根分别为t1,t2,则 ![]() ,
,
∴AB的长|AB|=|t1﹣t2|= ![]() =
= ![]() =
= ![]() ,
,
|PA||PB|=|t1t2|=3
【解析】(1)曲线C的极坐标方程转为ρ2=2ρcosθ+3,将ρ2=x2+y2 , ρcosθ=x代入,能求出曲线C的直角坐标方程;由直线l过定点P(1,1),且倾斜角为 ![]() ,能求出直线l的参数方程.(2)将直线l的参数方程代入x2+y2﹣2x﹣3=0,得
,能求出直线l的参数方程.(2)将直线l的参数方程代入x2+y2﹣2x﹣3=0,得 ![]() ,设方程两根分别为t1 , t2 , 利用韦达定理及弦长公式能求出|AB|及|PA||PB|的值.
,设方程两根分别为t1 , t2 , 利用韦达定理及弦长公式能求出|AB|及|PA||PB|的值.

练习册系列答案
相关题目
【题目】某校有教师400人,对他们进行年龄状况和学历的调查,其结果如下:
学历 | 35岁以下 | 35-55岁 | 55岁及以上 |
本科 |
| 60 | 40 |
硕士 | 80 | 40 |
|
(1)若随机抽取一人,年龄是35岁以下的概率为![]() ,求
,求![]() ;
;
(2)在35-55岁年龄段的教师中,按学历状况用分层抽样的方法,抽取一个样本容量为5的样本,然后在这5名教师中任选2人,求两人中至多有1人的学历为本科的概率.

