题目内容
15.已知△ABC各角的对应边分别为a,b,c,且满足$\frac{b}{a+c}$+$\frac{c}{a+b}$≥1,则角A的取值范围是(0,$\frac{π}{3}$].分析 将已知不等式化简整理,再由余弦定理,可得cosA≥$\frac{1}{2}$(0<A<π),再由余弦函数的单调性,即可得到A的范围.
解答 解:由$\frac{b}{a+c}$+$\frac{c}{a+b}$≥1,
可得,b(a+b)+c(a+c)≥(a+c)(a+b),
即b2+c2-a2≥bc,将不等式两边同除以2bc,
可得$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$≥$\frac{1}{2}$,
由余弦定理可得,cosA≥$\frac{1}{2}$(0<A<π)
所以0<A≤$\frac{π}{3}$.
故答案为:(0,$\frac{π}{3}$].
点评 本题考查余弦定理的运用,考查化简整理的能力,以及余弦函数的单调性的运用,属于中档题.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
5.目前我国很多城市出现了雾霾天气,已经给广大人民的健康带来影响,其中汽车尾气排放是造成雾霾天气的重要因素之一,很多城市提倡绿色出行方式,实施机动车尾号限行.某市为了解民众对“车辆限行”的态度,随机调查了50人,并半调查结果制成如表:
(1)若从年龄在[15,25)、[25,35)的被调查者中随机选取2人进行跟踪调查,记选中的4人中不赞成“车辆限行”的人数记为X,求X的分布列和期望;
(2)把年龄在[15,45)称为中青年,年龄在[45,75)称为中老年,请根据上表完成2×2列联表,并说明民众对“车辆限行”的态度与年龄是否有关联.
参考公式和数据:x2=$\frac{n(ad-bc)^{2}}{(a+c)(b+d)(a+b)(c+d)}$
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(2)把年龄在[15,45)称为中青年,年龄在[45,75)称为中老年,请根据上表完成2×2列联表,并说明民众对“车辆限行”的态度与年龄是否有关联.
| 态度 年龄 | 赞成 | 不赞成 | 总计 |
| 中青年 | |||
| 中老年 | |||
| 总计 |
| X2 | ≤2.706 | >2.706 | >3.841 | >6.635 |
| A、B关联性 | 无关联 | 90% | 95% | 99% |
20.已知随机变量X服从正态分布N(2,σ2),P(X≤3)=0.72,则P(1<X<3)等于( )
| A. | 0.28 | B. | 0.44 | C. | 0.56 | D. | 0.84 |
4.已知数列{an}为等差数列,若a3+a7=20,则数列{an}的前9项和S9等于( )
| A. | 40 | B. | 45 | C. | 60 | D. | 90 |
 为了解沈阳市高三学生某次模拟考试的数学成绩的某项指标,从所有成绩在及格线以上(90及90分以上)的考生中抽取一部分考生对其成绩进行统计,将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
为了解沈阳市高三学生某次模拟考试的数学成绩的某项指标,从所有成绩在及格线以上(90及90分以上)的考生中抽取一部分考生对其成绩进行统计,将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.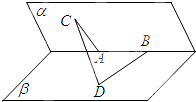 如图,已知是A,B是直二面角α-l-β的棱上两点,线段AC?α,线段BD?β,且AC⊥l,BD⊥l,AC=AB=6,BD=6$\sqrt{2}$,求线段CD的长.
如图,已知是A,B是直二面角α-l-β的棱上两点,线段AC?α,线段BD?β,且AC⊥l,BD⊥l,AC=AB=6,BD=6$\sqrt{2}$,求线段CD的长.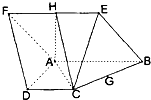 如图已知:菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H,G分别是线段EF,BC的中点.
如图已知:菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H,G分别是线段EF,BC的中点.