题目内容
7.已知a,b,c均为正数,且a+b+c=3,求证:$\frac{{b}^{2}}{a}$+$\frac{{c}^{2}}{b}$+$\frac{{a}^{2}}{c}$≥3.分析 利用综合法,直接证明不等式即可.
解答 证明:∵$\frac{{b}^{2}}{a}+a≥2b$,$\frac{{c}^{2}}{b}+b≥2c$,$\frac{{a}^{2}}{c}+c≥2a$.
∴$\frac{{b}^{2}}{a}$+$\frac{{c}^{2}}{b}$+$\frac{{a}^{2}}{c}$+(a+b+c)≥2(a+b+c),
即$\frac{{b}^{2}}{a}$+$\frac{{c}^{2}}{b}$+$\frac{{a}^{2}}{c}$≥a+b+c=3,当且仅当a=b=c=1时取等号.(10分)
点评 本题考查不等式的证明,综合法的应用,考查逻辑推理能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.半径为1的球内最大圆柱的体积为( )
| A. | $\frac{2\sqrt{6}}{9}$π | B. | $\frac{\sqrt{3}}{4}$π | C. | $\frac{2\sqrt{3}}{3}$π | D. | $\frac{4\sqrt{3}}{9}$π |
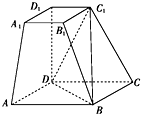 如图,在四棱台ABCD-A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=$\sqrt{2}$AD,AD=$\sqrt{2}$A1B1,∠BAD=45°.
如图,在四棱台ABCD-A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=$\sqrt{2}$AD,AD=$\sqrt{2}$A1B1,∠BAD=45°. 如图所示,已知平面α∥平面β,AB与CD是两条异面直线且AB?α,CD?β,如果E、F、G分别是AC、CB、BD的中点.求证:平面EFG∥α∥β.
如图所示,已知平面α∥平面β,AB与CD是两条异面直线且AB?α,CD?β,如果E、F、G分别是AC、CB、BD的中点.求证:平面EFG∥α∥β.