题目内容
4.已知数列{an}为等差数列,若a3+a7=20,则数列{an}的前9项和S9等于( )| A. | 40 | B. | 45 | C. | 60 | D. | 90 |
分析 利用等差数列的通项公式和前n项和公式求解.
解答 解:∵数列{an}为等差数列,a3+a7=20,
∴S9=$\frac{9({a}_{1}+{a}_{9})}{2}$=$\frac{9({a}_{3}+{a}_{7})}{2}$=$\frac{9×20}{2}$=90.
故选:D.
点评 本题考查等差数列的前9项和的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
16.半径为1的球内最大圆柱的体积为( )
| A. | $\frac{2\sqrt{6}}{9}$π | B. | $\frac{\sqrt{3}}{4}$π | C. | $\frac{2\sqrt{3}}{3}$π | D. | $\frac{4\sqrt{3}}{9}$π |
13.设0<θ<π,若cosθ+isinθ=$\frac{1+\sqrt{3}i}{-2i}$(i为虚数单位),则θ的值为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{π}{6}$ |
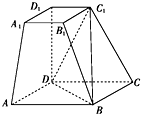 如图,在四棱台ABCD-A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=$\sqrt{2}$AD,AD=$\sqrt{2}$A1B1,∠BAD=45°.
如图,在四棱台ABCD-A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=$\sqrt{2}$AD,AD=$\sqrt{2}$A1B1,∠BAD=45°.