题目内容
3. 如图,已知是A,B是直二面角α-l-β的棱上两点,线段AC?α,线段BD?β,且AC⊥l,BD⊥l,AC=AB=6,BD=6$\sqrt{2}$,求线段CD的长.
如图,已知是A,B是直二面角α-l-β的棱上两点,线段AC?α,线段BD?β,且AC⊥l,BD⊥l,AC=AB=6,BD=6$\sqrt{2}$,求线段CD的长.
分析 A,B是直二面角α-l-β的棱上两点,线段AC?α,线段BD?β,且AC⊥l,BD⊥l,可得AC⊥BD.于是$\overrightarrow{CA}•\overrightarrow{AB}$=$\overrightarrow{CA}•\overrightarrow{BD}$=$\overrightarrow{AB}•\overrightarrow{BD}$=0.利用$\overrightarrow{CD}$=$\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BD}$,利用数量积运算性质即可得出.
解答 解:∵A,B是直二面角α-l-β的棱上两点,线段AC?α,线段BD?β,且AC⊥l,BD⊥l,∴AC⊥平面β,∴AC⊥BD.
∴$\overrightarrow{CA}•\overrightarrow{AB}$=$\overrightarrow{CA}•\overrightarrow{BD}$=$\overrightarrow{AB}•\overrightarrow{BD}$=0.
∵$\overrightarrow{CD}$=$\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BD}$,
∴${\overrightarrow{CD}}^{2}$=${\overrightarrow{CA}}^{2}+{\overrightarrow{AB}}^{2}+{\overrightarrow{BD}}^{2}$+$2\overrightarrow{CA}•\overrightarrow{AB}$+2$\overrightarrow{CA}•\overrightarrow{BD}$+2$\overrightarrow{AB}•\overrightarrow{BD}$=${6}^{2}+{6}^{2}+(6\sqrt{2})^{2}$=144,
∴$|\overrightarrow{CD}|$=12.
点评 本题考查了空间位置关系、向量数量积运算性质,考查了推理能力与计算能力,属于中档题.

| x | 2 | 3 | 4 | 5 |
| y | 2.2 | 3.8 | 5.5 | 6.5 |
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{π}{6}$ |
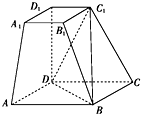 如图,在四棱台ABCD-A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=$\sqrt{2}$AD,AD=$\sqrt{2}$A1B1,∠BAD=45°.
如图,在四棱台ABCD-A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=$\sqrt{2}$AD,AD=$\sqrt{2}$A1B1,∠BAD=45°.