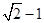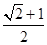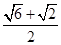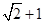题目内容
(本小题满分15分)
给定椭圆C: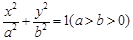 ,称圆心在原点O、半径是
,称圆心在原点O、半径是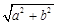 的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为
的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为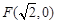 ,其短轴的一个端点到点
,其短轴的一个端点到点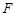 的距离为
的距离为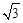 .
.
(1)求椭圆C和其“准圆”的方程;
(2)若点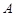 是椭圆C的“准圆”与
是椭圆C的“准圆”与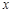 轴正半轴的交点,
轴正半轴的交点,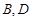 是椭圆C上的两相异点,且
是椭圆C上的两相异点,且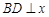 轴,求
轴,求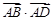 的取值范围;
的取值范围;
(3)在椭圆C的“准圆”上任取一点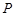 ,过点
,过点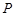 作直线
作直线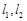 ,使得
,使得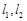 与椭圆C都只有一个交点,试判断
与椭圆C都只有一个交点,试判断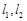 是否垂直?并说明理由.
是否垂直?并说明理由.
给定椭圆C:
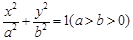 ,称圆心在原点O、半径是
,称圆心在原点O、半径是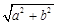 的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为
的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为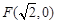 ,其短轴的一个端点到点
,其短轴的一个端点到点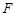 的距离为
的距离为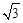 .
.(1)求椭圆C和其“准圆”的方程;
(2)若点
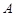 是椭圆C的“准圆”与
是椭圆C的“准圆”与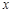 轴正半轴的交点,
轴正半轴的交点,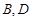 是椭圆C上的两相异点,且
是椭圆C上的两相异点,且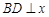 轴,求
轴,求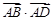 的取值范围;
的取值范围;(3)在椭圆C的“准圆”上任取一点
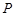 ,过点
,过点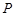 作直线
作直线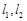 ,使得
,使得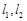 与椭圆C都只有一个交点,试判断
与椭圆C都只有一个交点,试判断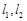 是否垂直?并说明理由.
是否垂直?并说明理由.(1)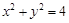 .(2)
.(2)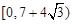 .(3)对于椭圆
.(3)对于椭圆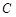 上的任意点
上的任意点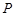 ,都有
,都有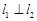 .
.
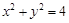 .(2)
.(2)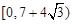 .(3)对于椭圆
.(3)对于椭圆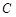 上的任意点
上的任意点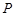 ,都有
,都有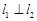 .
.试题分析:(1)由题意知
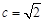 ,且
,且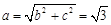 ,可得
,可得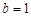 ,
,故椭圆C的方程为
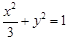 ,其“准圆”方程为
,其“准圆”方程为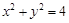 .
. (2)由题意,可设
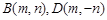
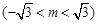 ,则有
,则有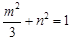 ,
,又A点坐标为
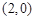 ,故
,故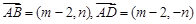 ,
,故
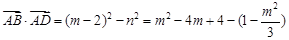
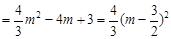 ,
, 又
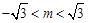 ,故
,故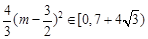 ,
, 所以
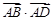 的取值范围是
的取值范围是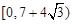 .
. (3)设
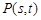 ,则
,则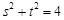 .
.当
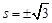 时,
时,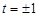 ,则
,则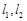 其中之一斜率不存在,另一斜率为0,显然有
其中之一斜率不存在,另一斜率为0,显然有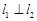 .
.当
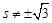 时,设过
时,设过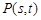 且与椭圆有一个公共点的直线
且与椭圆有一个公共点的直线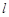 的斜率为
的斜率为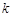 ,
,则
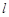 的方程为
的方程为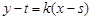 ,代入椭圆
,代入椭圆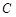 方程可得
方程可得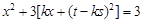 ,即
,即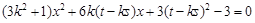 ,
,由
 ,
, 可得
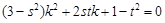 ,其中
,其中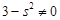 ,
, 设
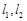 的斜率分别为
的斜率分别为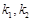 ,则
,则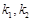 是上述方程的两个根,
是上述方程的两个根,故
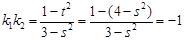 ,即
,即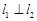 .
.综上可知,对于椭圆
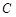 上的任意点
上的任意点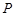 ,都有
,都有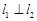 .
.点评:中档题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题新定义了“准圆”,解答时要注意审题,明确其特征。本题易漏“
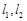 其中之一斜率不存在,另一斜率为0,
其中之一斜率不存在,另一斜率为0, 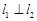 的情况。
的情况。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
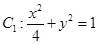 ,椭圆
,椭圆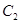 以
以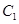 的长轴为短轴,且与
的长轴为短轴,且与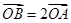 ,求直线
,求直线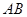 的方程.
的方程.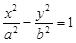 的焦距为10,点
的焦距为10,点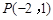 在其渐近线上,则双曲线的方程为
在其渐近线上,则双曲线的方程为
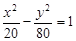

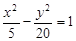
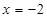 ,则抛物线方程是( )
,则抛物线方程是( )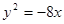 ,
,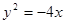
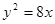
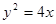
 上的动点,点P在y轴上的射影是M,点A的坐标是
上的动点,点P在y轴上的射影是M,点A的坐标是 ,则
,则 的最小值是
的最小值是

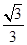 ,且与双曲线
,且与双曲线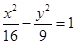 有相同的焦距,则椭圆的标准方程为________________________.
有相同的焦距,则椭圆的标准方程为________________________.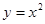 在点 处的切线平行于直线
在点 处的切线平行于直线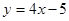 。
。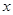 在轴上,离心率
在轴上,离心率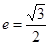 ,已知点
,已知点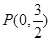 到这个椭圆上的最远距离是
到这个椭圆上的最远距离是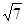 ,求这个椭圆的方程.
,求这个椭圆的方程.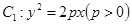 的焦点
的焦点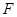 恰好是曲线
恰好是曲线 的右焦点,且曲线
的右焦点,且曲线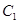 与曲线
与曲线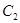 交点连线过点
交点连线过点