题目内容
设椭圆的中心是坐标原点,长轴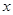 在轴上,离心率
在轴上,离心率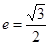 ,已知点
,已知点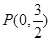 到这个椭圆上的最远距离是
到这个椭圆上的最远距离是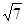 ,求这个椭圆的方程.
,求这个椭圆的方程.
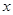 在轴上,离心率
在轴上,离心率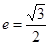 ,已知点
,已知点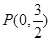 到这个椭圆上的最远距离是
到这个椭圆上的最远距离是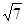 ,求这个椭圆的方程.
,求这个椭圆的方程.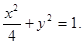
【错解分析】依题意可设椭圆方程为
 则
则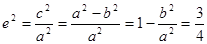 ,所以
,所以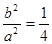 ,即
,即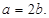 设椭圆上的点
设椭圆上的点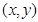 到点
到点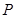 的距离为
的距离为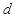 ,则
,则 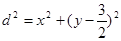
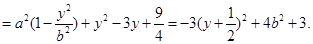 所以当
所以当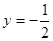 时,
时,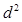 有最大值,从而
有最大值,从而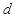 也有最大
也有最大值。所以
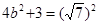 ,由此解得:
,由此解得: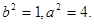 于是所求椭圆的方程为
于是所求椭圆的方程为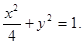
【正解】若
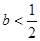 ,则当
,则当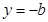 时,
时,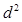 (从而
(从而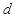 )有最大值.于是
)有最大值.于是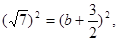 从而解得
从而解得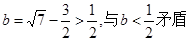 .所以必有
.所以必有 ,此时当
,此时当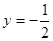 时,
时,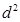 (从而
(从而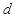 )有最大值,
)有最大值,所以
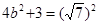 ,解得
,解得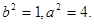 于是所求椭圆的方程为
于是所求椭圆的方程为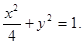

练习册系列答案
相关题目
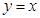 .抛物线
.抛物线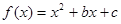 过B,D两点
过B,D两点 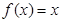 的两实根
的两实根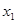 ,
,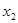 满足
满足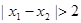
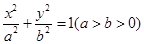 的离心率为
的离心率为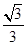 ,直线l: y-=x+2与.以原点为圆心、椭圆C1的短半轴长为半径的圆O相切.
,直线l: y-=x+2与.以原点为圆心、椭圆C1的短半轴长为半径的圆O相切.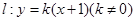 与椭圆
与椭圆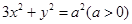 相交于
相交于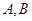 两个不同的点,与
两个不同的点,与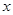 轴相交于点
轴相交于点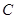 ,记
,记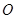 为坐标原点.
为坐标原点.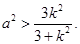
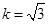 且
且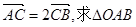 的面积及椭圆方程.
的面积及椭圆方程.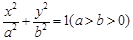 ,称圆心在原点O、半径是
,称圆心在原点O、半径是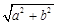 的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为
的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为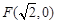 ,其短轴的一个端点到点
,其短轴的一个端点到点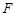 的距离为
的距离为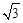 .
.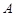 是椭圆C的“准圆”与
是椭圆C的“准圆”与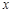 轴正半轴的交点,
轴正半轴的交点,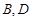 是椭圆C上的两相异点,且
是椭圆C上的两相异点,且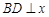 轴,求
轴,求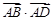 的取值范围;
的取值范围;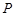 ,过点
,过点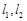 ,使得
,使得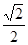 ,则该椭圆的方程为
,则该椭圆的方程为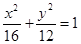
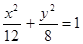
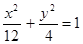
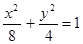
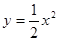 上的动点,点P在x轴上的射影为M,点A的坐标是
上的动点,点P在x轴上的射影为M,点A的坐标是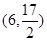 ,则
,则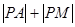 的最小值是( )
的最小值是( )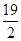
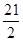
 中,
中,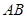 是半圆
是半圆 的直径,
的直径,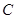 是半圆
是半圆 (除端点
(除端点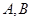 )上的任意一点.在线段
)上的任意一点.在线段 的延长线上取点
的延长线上取点 ,使
,使 ,试求动点
,试求动点
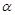 、
、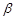 、
、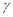 两两垂直,定点
两两垂直,定点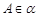 ,A到
,A到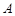 的距离,则P点轨迹上的点到
的距离,则P点轨迹上的点到