题目内容
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=1,AC=AA1=![]() , ∠ABC=60°.
, ∠ABC=60°.
(1)证明:AB⊥A1C;
(2)求二面角A﹣A1C﹣B的大小.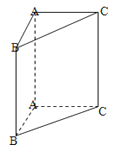
【答案】证明:(1)∵三棱柱ABC﹣A1B1C1为直三棱柱,∴AB⊥AA1 ,
在△ABC中,AB=1,AC=![]() ,∠ABC=60°,由正弦定理得∠ACB=30°,
,∠ABC=60°,由正弦定理得∠ACB=30°,
∴∠BAC=90°,即AB⊥AC,
∴AB⊥平面ACC1A1 ,
又A1C平面ACC1A1 ,
∴AB⊥A1C.
(2)解:如图,作AD⊥A1C交A1C于D点,连接BD,
由三垂线定理知BD⊥A1C,
∴∠ADB为二面角A﹣A1C﹣B的平面角.
在Rt△AA1C中,AD=![]() ,
,
在Rt△BAD中,tan∠ADB=![]() =
=![]() ,
,
∴cos∠ADB=![]() ,
,
即二面角A﹣A1C﹣B的大小为arccos![]() .
.
【解析】(1)欲证AB⊥A1C,而A1C平面ACC1A1 , 可先证AB⊥平面ACC1A1 , 根据三棱柱ABC﹣A1B1C1为直三棱柱,可知AB⊥AA1 , 由正弦定理得AB⊥AC,满足线面垂直的判定定理所需条件;
(2)作AD⊥A1C交A1C于D点,连接BD,由三垂线定理知BD⊥A1C,则∠ADB为二面角A﹣A1C﹣B的平面角,在Rt△BAD中,求出二面角A﹣A1C﹣B的余弦值即可.

练习册系列答案
相关题目
