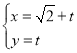题目内容
【题目】生活中人们常用“通五经贯六艺”形容一个人才识技艺过人，这里的“六艺”其实源于中国周朝的贵族教育体系，具体包括“礼、乐、射、御、书、数”.为弘扬中国传统文化，某校在周末学生业余兴趣活动中开展了“六艺”知识讲座，每艺安排一节，连排六节，则满足“数”必须排在前两节，“礼”和“乐”必须分开安排的概率为（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】
分情况讨论，由间接法得到“数”必须排在前两节，“礼”和“乐”必须分开的事件个数，不考虑限制因素，总数有
种，进而得到结果.
当“数”位于第一位时，礼和乐相邻有4种情况，礼和乐顺序有2种，其它剩下的有
种情况，由间接法得到满足条件的情况有
当“数”在第二位时，礼和乐相邻有3种情况，礼和乐顺序有2种，其它剩下的有种，
由间接法得到满足条件的情况有
共有：
种情况，不考虑限制因素，总数有种，
故满足条件的事件的概率为：
故答案为：C.
【题目】自从新型冠状病毒爆发以来，全国范围内采取了积极的措施进行防控，并及时通报各项数据以便公众了解情况，做好防护.以下是湖南省2020年1月23日-31日这9天的新增确诊人数.
日期 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
时间 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
新增确诊人数 | 15 | 19 | 26 | 31 | 43 | 78 | 56 | 55 | 57 |
经过医学研究，发现新型冠状病毒极易传染，一个病毒的携带者在病情发作之前通常有长达14天的潜伏期，这个期间如果不采取防护措施，则感染者与一位健康者接触时间超过15秒，就有可能传染病毒.
（1）将1月23日作为第1天，连续9天的时间作为变量x，每天新增确诊人数作为变量y，通过回归分析，得到模型
用于对疫情进行分析.对上表的数据作初步处理，得到下面的一些统计量的值（部分数据已作近似处理）：
，
.根据相关数据，求该模型的回归方程（结果精确到0.1），并依据该模型预测第10天新增确诊人数.
（2）如果一位新型冠状病毒的感染者传染给他人的概率为0.3，在一次12人的家庭聚餐中，只有一位感染者参加了聚餐，记余下的人员中被感染的人数为
，求
最有可能（即概率最大）的值是多少.
附：对于一组数据
，
…，
，其回归直线
的斜率和截距的最小二乘估计分别为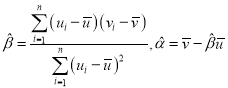
.
【题目】
甲、乙两个篮球运动员互不影响地在同一位置投球，命中率分别为
与
，且乙投球2次均未命中的概率为
.
（Ⅰ）求乙投球的命中率；
（Ⅱ）若甲投球1次，乙投球2次，两人共命中的次数记为
，求的分布列和数学期望.
【题目】某企业新研发了一种产品，产品的成本由原料成本及非原料成本组成.每件产品的非原料成本
（元）与生产该产品的数量
（千件）有关，经统计得到如下数据：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 112 | 61 | 44.5 | 35 | 30.5 | 28 | 25 | 24 |
根据以上数据，绘制了散点图.
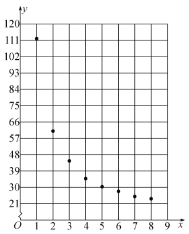
观察散点图，两个变量不具有线性相关关系，现考虑用反比例函数模型
和指数函数模型
分别对两个变量的关系进行拟合.已求得用指数函数模型拟合的回归方程为
，
与的相关系数
.
参考数据（其中
）：
|
|
|
|
|
|
|
|
183.4 | 0.34 | 0.115 | 1.53 | 360 | 22385.5 | 61.4 | 0.135 |
（1）用反比例函数模型求关于的回归方程；
（2）用相关系数判断上述两个模型哪一个拟合效果更好（精确到0.01），并用其估计产量为10千件时每件产品的非原料成本；
（3）该企业采取订单生产模式（根据订单数量进行生产，即产品全部售出）.根据市场调研数据，若该产品单价定为100元，则签订9千件订单的概率为0.8，签订10千件订单的概率为0.2；若单价定为90元，则签订10千件订单的概率为0.3，签订11千件订单的概率为0.7.已知每件产品的原料成本为10元，根据（2）的结果，企业要想获得更高利润，产品单价应选择100元还是90元，请说明理由.
参考公式：对于一组数据
，
，…，
，其回归直线
的斜率和截距的最小二乘估计分别为：
，
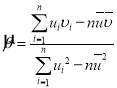，相关系数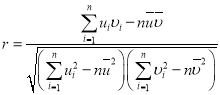
.