Question

【题目】过抛物线的焦点的直线与抛物线交于，两点，若，在准线上的射影为，，则等于(　　)．

A. B. C. D.

Answer 1

【答案】D

【解析】

由抛物线的定义及内错角相等，可得∠AFA1=∠A1FK，同理可证∠BFB1=∠B1FK，由∠AFA1+∠A1FK+∠BFB1+∠B1FK=180°，可得答案．

解答：解：如图：

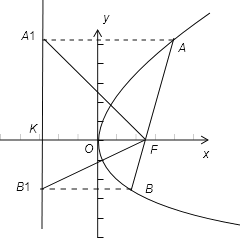
设准线与x轴的交点为K，∵A、B在抛物线的准线上的射影为A1、B1，

由抛物线的定义可得，AA1=AF，∴∠AA1F=∠AFA1，又由内错角相等得∠AA1F=∠A1FK，∴∠AFA1=∠A1FK．

同理可证∠BFB1=∠B1FK． 由∠AFA1+∠A1FK+∠BFB1+∠B1FK=180°，

∴∠A1FK+∠B1FK=∠A1FB1=90°，

故选D．