题目内容
【题目】已知数列{an}为等差数列,a1=2,{an}的前n项和为Sn , 数列{bn}为等比数列,且a1b1+a2b2+a3b3+…+anbn=(n﹣1)2n+2+4对任意的n∈N*恒成立.
(1)求数列{an}、{bn}的通项公式;
(2)是否存在非零整数λ,使不等式sin ![]() <
< ![]() 对一切n∈N*都成立?若存在,求出λ的值;若不存在,说明理由.
对一切n∈N*都成立?若存在,求出λ的值;若不存在,说明理由.
(3)各项均为正整数的无穷等差数列{cn},满足c39=a1007 , 且存在正整数k,使c1 , c39 , ck成等比数列,若数列{cn}的公差为d,求d的所有可能取值之和.
【答案】
(1)解:设数列{an}的公差为d,数列{bn}的公比为q,
∵a1b1+a2b2+a3b3+…+anbn=(n﹣1)2n+2+4,
令n=1,2,3,分别得a1b1=4,a1b1+a2b2=20,a1b1+a2b2+a3b3=68,
又a1=2,
∴ 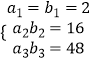 ,即
,即 ![]() ,解得
,解得 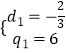 或
或 ![]() .
.
经检验d=q=2符合题意, ![]() 不合题意,舍去.
不合题意,舍去.
∴an=2n, ![]() ;
;
(2)解:由an=2n,得sin ![]() ,
,
设 ![]() ,
,
则不等式sin ![]() <
< ![]() 等价于
等价于 ![]() ,
,
∵bn>0,且 ![]() ,
,
∴bn+1>bn,数列{bn}单调递增,
假设存在这样的实数λ,使得不等式 ![]() 对一切n∈N*都成立,则
对一切n∈N*都成立,则
①当n=4m+4和n=4m+2,m∈N时,sin ![]() ,不等式
,不等式 ![]() 恒成立;
恒成立;
②当n=4m+1,m∈N时,sin ![]() ,λ<
,λ< ![]() ;
;
③当n=4m+3,m∈N时,sin ![]() ,
, ![]() .
.
综上,λ∈( ![]() ),由λ是非0整数,可知存在λ=1(﹣1不满足题意,舍)满足条件;
),由λ是非0整数,可知存在λ=1(﹣1不满足题意,舍)满足条件;
(3)解:由题意可知,d=0时成立;
当d>0时,c39=c1+38d=2014,得c1=2014﹣38d.
ck=c39+(k﹣39)d=2014+(k﹣39)d,
由 ![]() ,得(2014﹣38d)[014+(k﹣39)d]=20142,得
,得(2014﹣38d)[014+(k﹣39)d]=20142,得
k= ![]() =
= ![]() =
= ![]() ∈N*.
∈N*.
又∵ ![]() ,0<53﹣d<53.
,0<53﹣d<53.
∴53﹣d=1,2,19,53,
则d=0,52,51,34,
∴公差d的所有可能取值之和为137.
【解析】(1)设数列{an}的公差为d,数列{bn}的公比为q,在a1b1+a2b2+a3b3+…+anbn=(n﹣1)2n+2+4中分别令n=1,2,3,得到关于d与q的方程组,求解方程组可得 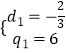 或
或 ![]() ,检验d=q=2符合题意,从而求得an=2n,
,检验d=q=2符合题意,从而求得an=2n, ![]() ;(2)由an=2n,得sin
;(2)由an=2n,得sin ![]() ,设
,设 ![]() ,把原不等式转化为
,把原不等式转化为 ![]() ,且
,且 ![]() ,可得数列{bn}单调递增,假设存在这样的实数λ,使得不等式
,可得数列{bn}单调递增,假设存在这样的实数λ,使得不等式 ![]() 对一切n∈N*都成立,分①n=4m+4和n=4m+2,m∈N,②n=4m+1,m∈N,③n=4m+3,m∈N时求解非0整数λ的值;(3)由题意可知,d=0时成立;当d>0时,结合
对一切n∈N*都成立,分①n=4m+4和n=4m+2,m∈N,②n=4m+1,m∈N,③n=4m+3,m∈N时求解非0整数λ的值;(3)由题意可知,d=0时成立;当d>0时,结合 ![]() ,得(2014﹣38d)[2014+(k﹣39)d]=20142 , 即k=
,得(2014﹣38d)[2014+(k﹣39)d]=20142 , 即k= ![]() =
= ![]() =
= ![]() ∈N* . 再由d>0且c1>0求出λ的所有可能取值得答案.
∈N* . 再由d>0且c1>0求出λ的所有可能取值得答案.
【考点精析】根据题目的已知条件,利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系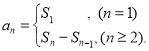 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.