题目内容
【题目】若数列![]() 对任意连续三项
对任意连续三项![]() ,均有
,均有![]() ,则称该数列为“跳跃数列”.
,则称该数列为“跳跃数列”.
(1)判断下列两个数列是否是跳跃数列:
①等差数列:![]() ;
;
②等比数列:![]() ;
;
(2)若数列![]() 满足对任何正整数
满足对任何正整数![]() ,均有
,均有![]()
![]() .证明:数列
.证明:数列![]() 是跳跃数列的充分必要条件是
是跳跃数列的充分必要条件是![]() .
.
(3)跳跃数列![]() 满足对任意正整数
满足对任意正整数![]() 均有
均有![]() ,求首项
,求首项![]() 的取值范围.
的取值范围.
【答案】(1)① 等差数列:![]() 不是跳跃数列;② 等比数列:
不是跳跃数列;② 等比数列:![]() 是跳跃数列.(2)证明见解析(3)
是跳跃数列.(2)证明见解析(3)![]()
【解析】
(1)①数列通项公式为![]() ,计算可得:
,计算可得:![]() ,所以它不是跳跃数列;②数列通项公式为:
,所以它不是跳跃数列;②数列通项公式为: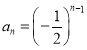 ,计算可得:
,计算可得:![]() ,所以它是跳跃数列;
,所以它是跳跃数列;
(2)必要性:若![]() ,则
,则![]() 是单调递增数列,若
是单调递增数列,若![]() ,
,![]() 是常数列,均不是跳跃数列;充分性:用数学归纳法证明证明,
是常数列,均不是跳跃数列;充分性:用数学归纳法证明证明,![]() 命题成立,若
命题成立,若![]() 时
时![]() ,可得:
,可得:![]() ,所以当
,所以当![]() 时命题也成立;
时命题也成立;
(3)有已知可得:![]()
![]() ,
,![]()
![]() ,若
,若![]() ,则
,则![]() ,解得
,解得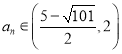 ;若
;若![]() ,则
,则![]() ,解得
,解得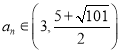 ,
,
由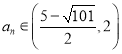 ,则
,则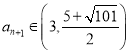 ,得
,得![]() ;当
;当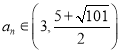 ,则
,则![]() ,得
,得![]() ,问题得解.
,问题得解.
(1)①等差数列:![]() 通项公式为:
通项公式为:![]()
![]()
所以此数列不是跳跃数列;
②等比数列:![]() 通项公式为:
通项公式为: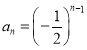
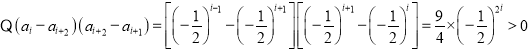
所以此数列是跳跃数列
(2)必要性:
若![]() ,则
,则![]() 是单调递增数列,不是跳跃数列;
是单调递增数列,不是跳跃数列;
若![]() ,
,![]() 是常数列,不是跳跃数列.
是常数列,不是跳跃数列.
充分性:(下面用数学归纳法证明)
若![]() ,则对任何正整数
,则对任何正整数![]() ,均有
,均有![]() 成立.
成立.
![]() 当
当![]() 时,
时,![]() ,
, ![]() ,
,
![]() ,
,![]()
![]() ,
,
所以![]() 命题成立
命题成立
![]() 若
若![]() 时,
时,![]() ,
,
则![]() ,
,
![]() ,
,
所以当![]() 时命题也成立,
时命题也成立,
根据数学归纳法,可知命题成立,数列满足![]() ,
,
故![]() 是跳跃数列.
是跳跃数列.
(3)![]()
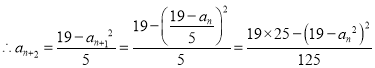
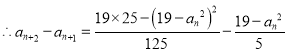
![]()
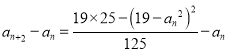
![]()
![]() 若
若![]() ,则
,则![]() ,
,
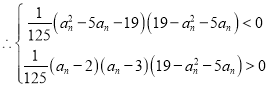
解得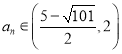 ;
;
![]() 若
若![]() ,则
,则![]() ,
,
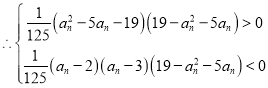
解得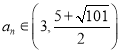 ;
;
若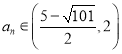 ,则
,则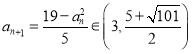 ,所以
,所以![]() ,
,
若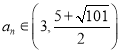 ,则
,则![]() ,所以
,所以![]() ,
,
所以![]() ,
,
此时对任何正整数![]() ,均有
,均有![]()

【题目】高中生在被问及“家,朋友聚集的地方,个人空间”三个场所中“感到最幸福的场所在哪里?”这个问题时,从洛阳的高中生中,随机抽取了55人,从上海的高中生中随机抽取了45人进行答题.洛阳高中生答题情况是:选择家的占![]() 、选择朋友聚集的地方的占
、选择朋友聚集的地方的占![]() 、选择个人空间的占
、选择个人空间的占![]() .上海高中生答题情况是:选择朋友聚集的地方的占
.上海高中生答题情况是:选择朋友聚集的地方的占![]() 、选择家的占
、选择家的占![]() 、选择个人空间的占
、选择个人空间的占![]() .
.
(1)请根据以上调查结果将下面![]() 列联表补充完整,并判断能否有
列联表补充完整,并判断能否有![]() 的把握认为“恋家(在家里感到最幸福)”与城市有关:
的把握认为“恋家(在家里感到最幸福)”与城市有关:
在家里最幸福 | 在其它场所最幸福 | 合计 | |
洛阳高中生 | |||
上海高中生 | |||
合计 |
(2) 从被调查的不“恋家”的上海学生中,用分层抽样的方法选出4人接受进一步调查,从被选出的4 人中随机抽取2人到洛阳交流学习,求这2人中含有在“个人空间”感到幸福的学生的概率.
附:![]() ,其中
,其中![]() d.
d.