题目内容
18.已知△ABC中,∠A,∠B,∠C的对边分别为a,b,c,若a=1,2cosC+c=2b,则△ABC的周长的最大值是3.分析 由余弦定理求得cosC,代入已知等式可得(b+c)2-1=3bc,利用基本不等式求得b+c≤2,故a+b+c≤3.
解答 解:△ABC中,由余弦定理可得2cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{ab}$,
∵a=1,2cosC+c=2b,
∴$\frac{1+{b}^{2}-{c}^{2}}{b}$+c=2b,化简可得(b+c)2-1=3bc.
∵bc≤$(\frac{b+c}{2})^{2}$,∴(b+c)2-1≤3×$(\frac{b+c}{2})^{2}$,解得:b+c≤2(当且仅当b=c时,取等号).
∴△ABC的周长的最大值是3.
故答案为:3.
点评 本题主要考查余弦定理、基本不等式的应用,考查学生的灵活变形能力,属于中档题.

练习册系列答案
相关题目
6.执行如图所示的程序框图,如果输入的x∈[-1,3],则输出的y属于( )
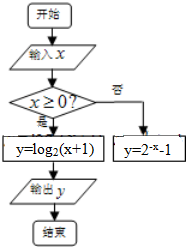

| A. | [0,2] | B. | [1,2] | C. | [0,1] | D. | [-1,5] |
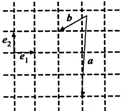 已知向量$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$、$\overrightarrow{a}$、$\overrightarrow{b}$如图所示,以$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$为基底,则$\overrightarrow{a}$-$\overrightarrow{b}$可表示为$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$.
已知向量$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$、$\overrightarrow{a}$、$\overrightarrow{b}$如图所示,以$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$为基底,则$\overrightarrow{a}$-$\overrightarrow{b}$可表示为$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$.