题目内容
2.已知f(x)=lnx-ex+a.(1)若x=1是f(x)的极值点,讨论f(x)的单调性;
(2)当a≥-2时,证明f(x)在定义域内无零点.
分析 (1)求导函数,利用x=1是f(x)的极值点,求出a的值,再利用导数的正负,即可得出f(x)的单调性
(2)a≥-2时,ex+a≥ex-2,lnx-ex+a≤lnx-ex-2,只需证明g(x)=lnx-ex-2<0,求出g(x)max<0,即可得出结论.
解答 (1)解:∵f(x)=lnx-ex+a,
∴f′(x)=$\frac{1}{x}$-ex+a,
∵x=1是f(x)的极值点,
∴1-e1+a=0,
∴a=-1,
∴f′(x)=$\frac{1}{x}$-ex-1,
x∈(0,1)时,f′(x)>0,f(x)在(0,1)内单调递增,当x∈(1,+∞)时,f′(x)<0,f(x)在(1,+∞)内单调递减;
(2)证明:当a≥-2时,ex+a≥ex-2,lnx-ex+a≤lnx-ex-2,
令g(x)=lnx-ex-2.
∵g′(x)=$\frac{1}{x}$-ex-2,
由g′(x)=0得$\frac{1}{x}$=ex-2,方程有唯一解x0∈(1,2),
∴x∈(0,x0)时,g′(x)>0,g(x)在(0,x0)内单调递增,
x∈(x0,+∞)时,g′(x)<0,g(x)在(x0,+∞)内单调递减,
∴g(x)max=lnx0-ex0-2=-x0+2-$\frac{1}{{x}_{0}}$
∵x0∈(1,2),
∴x0+$\frac{1}{{x}_{0}}$>2,
∴g(x)max<0
综上,当a≥-2时,f(x)<0,
∴f(x)在定义域内无零点.
点评 本题考查导数知识的运用,考查函数的单调性,考查函数的最值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
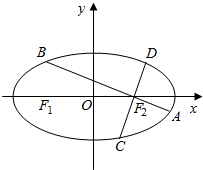 如图,已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,过椭圆右焦点F2作两条互相垂直的弦AB与CD,当直线AB的斜率为0时,|AB|+|CD|=7.
如图,已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,过椭圆右焦点F2作两条互相垂直的弦AB与CD,当直线AB的斜率为0时,|AB|+|CD|=7.