题目内容
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() ,
,![]() 的值:
的值:
(2)求证:当![]() 时,
时,![]() 在
在![]() 上有两个极值点:
上有两个极值点:
(3)设![]() ,若
,若![]() 在
在![]() 单调递减,求实数
单调递减,求实数![]() 的取值范围.(其中
的取值范围.(其中![]() 为自然对数的底数)
为自然对数的底数)
【答案】(1)![]() ;
;![]() .(2)见解析(3)
.(2)见解析(3)![]()
【解析】
(1)根据函数解析式,先求得导函数,将横坐标带入结合切线方程的斜率即可求得![]() 的值,进而可得切点坐标,将切点坐标代入切线方程即可得
的值,进而可得切点坐标,将切点坐标代入切线方程即可得![]() 的值.
的值.
(2)令![]() ,再求得
,再求得![]() ,由导函数与函数单调性关系可得
,由导函数与函数单调性关系可得![]() 的单调区间.由
的单调区间.由![]() 可得
可得![]() 的最小值符号,再由
的最小值符号,再由![]() 及零点存在定理可判断
及零点存在定理可判断![]() 在
在![]() 有一个零点
有一个零点![]() ;表示出
;表示出![]() ,并构造函数
,并构造函数![]() ,由
,由![]() 的符号可得
的符号可得![]() 的单调递减区间,根据零点存在定理可知
的单调递减区间,根据零点存在定理可知![]() 在
在![]() 有一个零点
有一个零点![]() ,从而证明出结论.
,从而证明出结论.
(3)由题意可得![]() 的表达式,构造函数
的表达式,构造函数![]() ,并求得
,并求得![]() ,再构造函数
,再构造函数![]() ,并由
,并由![]() 的符号可判断
的符号可判断![]() 的单调情况,从而由
的单调情况,从而由![]() 的最值判断出
的最值判断出![]() 的符号,即可得
的符号,即可得![]() 的单调情况.对
的单调情况.对![]() 分类讨论,从而由
分类讨论,从而由![]() 的符号得符合题意的
的符号得符合题意的![]() 的取值范围.
的取值范围.
(1)函数![]() .
.
则![]() ,
,
由条件知![]() ,所以
,所以![]() ,
,
![]() ,所以切点坐标为
,所以切点坐标为![]() .
.
把![]() 代入
代入![]() ,
,
解得![]() .
.
(2)证明:令![]() ,
,
则![]() ,所以
,所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
因为![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() 在
在![]() 有一个零点
有一个零点![]() .
.
又![]() ,
,
令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 单调递减,故
单调递减,故![]() ,
,
即![]() ,所以
,所以![]() 在
在![]() 有一个零点
有一个零点![]() .
.
于是可知:当![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,
![]() ,
,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
因此,![]() 在
在![]() 上有两个极值点(在
上有两个极值点(在![]() 处取得极大值,在
处取得极大值,在![]() 处取得极小值).
处取得极小值).
(3)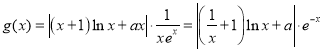 ,
,
令![]() ,
,
则![]() ,
,
令![]() ,当
,当![]() 时,
时,![]() ,
,
![]() 单调递增,
单调递增,![]() ,
,
所以![]() ,
,![]() 在
在![]() 单调递增,
单调递增,
于是可得![]() ,
,
①若![]() ,则
,则![]() ,
,![]() ,
,
因为![]() 在
在![]() 单调递减,
单调递减,
所以![]()
![]() ,
,
令![]() ,
,
当![]() 时,
时,![]() ,
,
故![]() 单调递减,所以
单调递减,所以![]() ,解得
,解得![]() ,
,
②若![]() ,则
,则![]() ,
,
![]() ,
,
因为![]() 在
在![]() 单调递减,所以
单调递减,所以![]() ,
,
当![]() ,
,![]() 时,
时,
![]() ,
,
所以![]() ,即
,即![]() ,满足题设.
,满足题设.
③若![]() ,则存在唯一确定的
,则存在唯一确定的![]() ,使得
,使得![]() .
.
当![]() 时,
时,![]() ,即存在
,即存在![]() ,
,![]() ,
,
但![]() ,这与
,这与![]() 在
在![]() 单调递减矛盾,不合题意.
单调递减矛盾,不合题意.
综上所述,![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某药业公司统计了2010-2019年这10年某种疾病的患者人数,结论如下:该疾病全国每年的患者人数都不低于100万,其中有3年的患者人数低于200万,有6年的患者人数不低于200万且低于300万,有1年的患者人数不低于300万.
(1)药业公司为了解一新药品对该疾病的疗效,选择了200名患者,随机平均分为两组作为实验组和对照组,实验结束时,有显著疗效的共110人,实验组中有显著疗效的比率为70%.请完成如下的2×2列联表,并根据列联表判断是否有99.9%把握认为该药品对该疾病有显著疗效;
实验组 | 对照组 | 合计 | |
有显著疗效 | |||
无显著疗效 | |||
合计 | 200 |
(2)药业公司最多能引进3条新药品的生产线,据测算,公司按如下条件运行生产线:
该疾病患者人数(单位:万) |
|
|
|
最多可运行生产线数 | 1 | 2 | 3 |
每运行一条生产线,可产生年利润6000万元,没运行的生产线毎条每年要亏损1000万元.根据该药业公司这10年的统计数据,将患者人数在以上三段的频率视为相应段的概率、假设各年的患者人数相互独立.欲使该药业公司年总利润的期望值达到最大,应引进多少条生产线?
附:参考公式: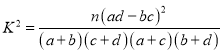 ,其中
,其中![]() .
.
| 0.05 | 0.025 | 0.010 | 0.001 |
| 3.841 | 5.024 | 6.635 | 10.828 |
