题目内容
10．已知△ABC的周长等于20，面积是10$\sqrt{3}$，A=60°，则A的对边长为7．分析 由题意可得，a+b+c=20，由三角形的面积公式可得S=$\frac{1}{2}bcsin60°$，结合已知可求bc，然后由余弦定理，a2=b2+c2-2bccos60°可求a
解答 解：由题意可得，a+b+c=20，
∵S=$\frac{1}{2}bcsin60°$=10$\sqrt{3}$，
∴bc=40，
由余弦定理可得，a2=b2+c2-2bccos60°=（b+c）2-3bc=（20-a）2-120
解方程可得，a=7
故答案为：7
点评 本题主要考查了三角形的面积公式及余弦定理在求解三角形中的应用，属于基础试题．
练习册系列答案
阅读快车系列答案
相关题目
5．在△ABC中，AB=3，BC=$\sqrt{13}$，AC=4，则AC边上的高等于（ ）
| A． | $\frac{3}{2}$$\sqrt{3}$ | B． | $\frac{3}{2}$$\sqrt{2}$ | C． | 3 | D． | 3$\sqrt{3}$ |
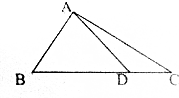已知在△ABC中，点D在BC上，且满足$\overrightarrow{BD}$=3$\overrightarrow{DC}$，若$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$，则x+y=1．