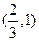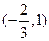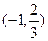题目内容
设函数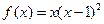 ,
,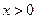 .
.
⑴求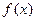 的极值;
的极值;
(2)设函数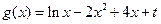 (
(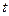 为常数),若使
为常数),若使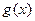 ≤
≤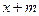 ≤
≤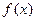 在
在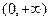 上恒成立的实数
上恒成立的实数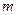 有且只有一个,求实数
有且只有一个,求实数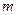 和
和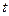 的值;
的值;
(3)讨论方程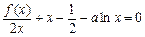 的解的个数,并说明理由.
的解的个数,并说明理由.
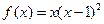 ,
,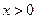 .
.⑴求
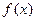 的极值;
的极值;(2)设函数
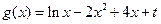 (
(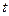 为常数),若使
为常数),若使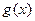 ≤
≤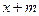 ≤
≤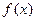 在
在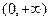 上恒成立的实数
上恒成立的实数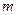 有且只有一个,求实数
有且只有一个,求实数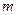 和
和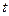 的值;
的值;(3)讨论方程
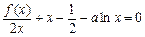 的解的个数,并说明理由.
的解的个数,并说明理由.解:⑴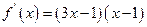 令
令 ,得
,得 ,
,
 区间
区间 分别单调增,单调减,单调增,
分别单调增,单调减,单调增,
于是当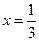 时,有极大值
时,有极大值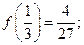
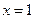 时,有极小值
时,有极小值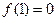 ;
;
(2)由已知得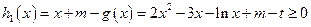 在
在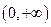 上恒成立,
上恒成立,
由 得
得 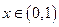 时,
时, ,
, 时,
时, ,
,
故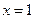 时,函数
时,函数 取到最小值.从而
取到最小值.从而 ;
;
同样的, 在
在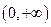 上恒成立,
上恒成立,
由 得
得 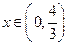 时,
时, ;
;  时,
时,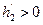 ,
,
故 时,函数
时,函数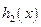 取到最小值. 从而
取到最小值. 从而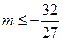 ,
,
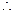
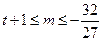
由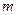 的唯一性知
的唯一性知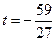 ,
,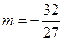 ;
;
(3)记
 =
=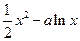
①当 时,
时,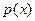 在定义域
在定义域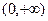 上恒大于
上恒大于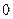 ,此时方程无解;
,此时方程无解;
②当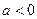 时,
时,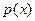 在定义域
在定义域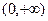 上为增函数.
上为增函数.
 ,
,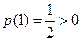 ,所以,此时方程有唯一解。
,所以,此时方程有唯一解。
③当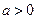 时,
时, ,
,
当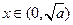 时,
时,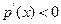 ,所以
,所以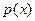 在
在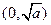 为减函数
为减函数
当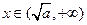 时,
时,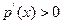 ,所以
,所以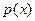 在
在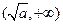 为增函数
为增函数
所以,当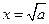 时,
时,

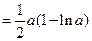
(a)当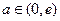 时,
时,  ,所以,此时方程无解
,所以,此时方程无解
(b)当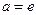 时,
时, 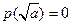 ,所以,此时方程有唯一解
,所以,此时方程有唯一解
(c)当 时,
时,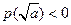 ,
,
因为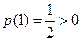 且
且 ,所以方程在区间
,所以方程在区间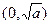 上有唯一解,
上有唯一解,
因为当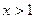 时,
时, ,所以
,所以 
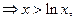
所以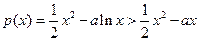
因为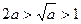 ,所以
,所以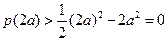
所以 方程在区间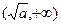 上有唯一解.
上有唯一解.
所以,此时方程有两解.
综上所述:当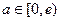 时, 方程无解;
时, 方程无解;
当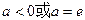 时, 方程有唯一解;
时, 方程有唯一解;
当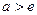 时, 方程有两解 。
时, 方程有两解 。
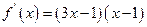 令
令 ,得
,得 ,
, 区间
区间 分别单调增,单调减,单调增,
分别单调增,单调减,单调增,于是当
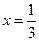 时,有极大值
时,有极大值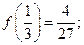
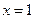 时,有极小值
时,有极小值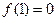 ;
;(2)由已知得
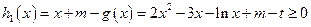 在
在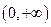 上恒成立,
上恒成立,由
 得
得 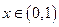 时,
时, ,
, 时,
时, ,
,故
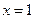 时,函数
时,函数 取到最小值.从而
取到最小值.从而 ;
;同样的,
 在
在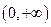 上恒成立,
上恒成立,由
 得
得 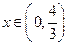 时,
时, ;
;  时,
时,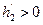 ,
,故
 时,函数
时,函数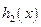 取到最小值. 从而
取到最小值. 从而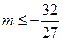 ,
,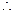
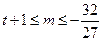
由
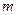 的唯一性知
的唯一性知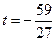 ,
,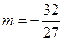 ;
;(3)记

 =
=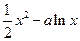
①当
 时,
时,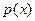 在定义域
在定义域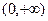 上恒大于
上恒大于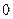 ,此时方程无解;
,此时方程无解; ②当
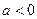 时,
时,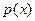 在定义域
在定义域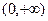 上为增函数.
上为增函数. ,
,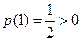 ,所以,此时方程有唯一解。
,所以,此时方程有唯一解。③当
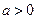 时,
时, ,
,当
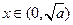 时,
时,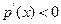 ,所以
,所以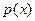 在
在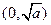 为减函数
为减函数当
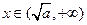 时,
时,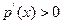 ,所以
,所以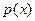 在
在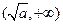 为增函数
为增函数所以,当
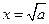 时,
时,

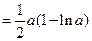
(a)当
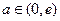 时,
时,  ,所以,此时方程无解
,所以,此时方程无解(b)当
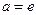 时,
时, 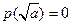 ,所以,此时方程有唯一解
,所以,此时方程有唯一解(c)当
 时,
时,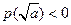 ,
,因为
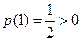 且
且 ,所以方程在区间
,所以方程在区间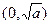 上有唯一解,
上有唯一解, 因为当
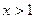 时,
时, ,所以
,所以 
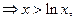
所以
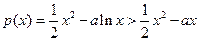
因为
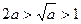 ,所以
,所以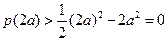
所以 方程在区间
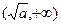 上有唯一解.
上有唯一解.所以,此时方程有两解.
综上所述:当
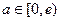 时, 方程无解;
时, 方程无解;当
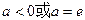 时, 方程有唯一解;
时, 方程有唯一解; 当
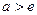 时, 方程有两解 。
时, 方程有两解 。略

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
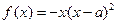 (
(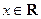 ),其中
),其中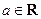 .
.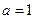 时,求曲线
时,求曲线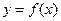 在点
在点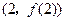 处的切线方程;
处的切线方程;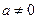 时,求函数
时,求函数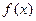 的极大值和极小值;
的极大值和极小值;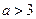 ,
, 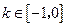 时,若不等式
时,若不等式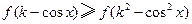 对任意的
对任意的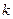 的值。
的值。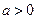 ,函数
,函数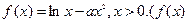 的图像连续不断)
的图像连续不断)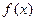 的单调区间;
的单调区间;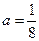 时,证明:存在
时,证明:存在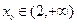 ,使
,使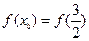 ;
;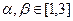 ,且
,且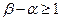 ,使
,使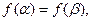 证明
证明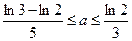 .
.
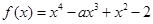 有且仅有一个极值点,则实数
有且仅有一个极值点,则实数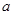 的取值范围 ( )
的取值范围 ( ) ,
, 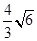 ]
]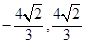 ]
]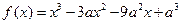 .
.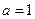 ,求函数
,求函数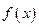 的极值;
的极值; ,且当
,且当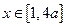 时,
时,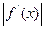
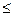 12a恒成立,试确定
12a恒成立,试确定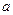 的取值范围.
的取值范围.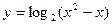 的递增区间是:________________
的递增区间是:________________
 的解集是
的解集是 ;②不等式
;②不等式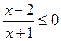 的解集是
的解集是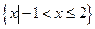 ;③
;③ 的最小值为
的最小值为 ;④在
;④在 中
中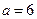 ,
, ,
, 有两解,其中正确命题的序号是
有两解,其中正确命题的序号是 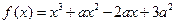 ,且在
,且在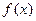 图象上点
图象上点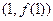 处的切线在y轴上的截距小于0,则a的取值范围是 ( )
处的切线在y轴上的截距小于0,则a的取值范围是 ( )