题目内容
(本小题满分14分)
已知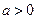 ,函数
,函数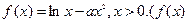 的图像连续不断)
的图像连续不断)
(Ⅰ)求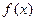 的单调区间;
的单调区间;
(Ⅱ)当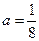 时,证明:存在
时,证明:存在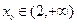 ,使
,使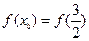 ;
;
(Ⅲ)若存在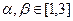 ,且
,且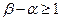 ,使
,使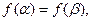 证明
证明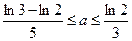 .
.
已知
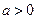 ,函数
,函数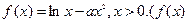 的图像连续不断)
的图像连续不断)(Ⅰ)求
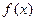 的单调区间;
的单调区间;(Ⅱ)当
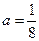 时,证明:存在
时,证明:存在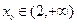 ,使
,使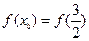 ;
;(Ⅲ)若存在
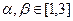 ,且
,且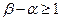 ,使
,使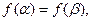 证明
证明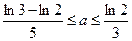 .
.
(I)解: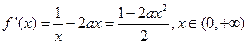 , …………2分
, …………2分
令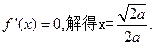 …………………3分
…………………3分
当x变化时,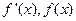 的变化情况如下表:
的变化情况如下表:
所以,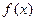 的单调递增区间是
的单调递增区间是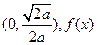 的单调递减区间是
的单调递减区间是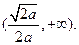 ……6分
……6分
(II)证明:当
由(I)知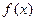 在(0,2)内单调递增, 在
在(0,2)内单调递增, 在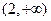 内单调递减. ………7分
内单调递减. ………7分
令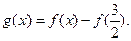
由于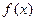 在(0,2)内单调递增,
在(0,2)内单调递增,
故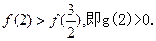 …………………8分
…………………8分
取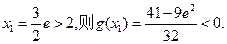
所以 存在
存在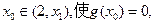
即存在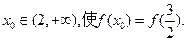 ………………10分
………………10分
(说明: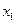 的取法不唯一,只要满
的取法不唯一,只要满 足
足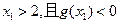 即可)
即可)
(III)证明:由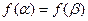 及(I)的结论知
及(I)的结论知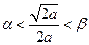 ,
,
从而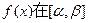 上的最小值为
上的最小值为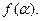 ……………………11分
……………………11分
又由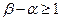 ,
,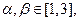 知
知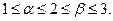
故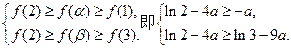 …………13分
…………13分
从而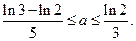 ……………………………………14分
……………………………………14分
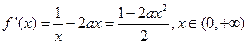 , …………2分
, …………2分令
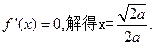 …………………3分
…………………3分当x变化时,
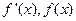 的变化情况如下表:
的变化情况如下表: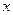 | 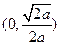 | 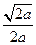 | 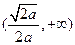 |
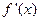 | + | 0 | 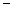 |
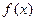 |   | 极大值 | 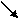 |
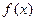 的单调递增区间是
的单调递增区间是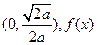 的单调递减区间是
的单调递减区间是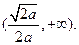 ……6分
……6分(II)证明:当

由(I)知
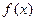 在(0,2)内单调递增, 在
在(0,2)内单调递增, 在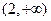 内单调递减. ………7分
内单调递减. ………7分令
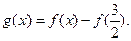
由于
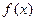 在(0,2)内单调递增,
在(0,2)内单调递增,故
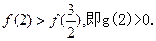 …………………8分
…………………8分取
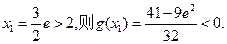
所以
 存在
存在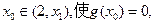
即存在
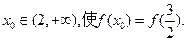 ………………10分
………………10分(说明:
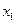 的取法不唯一,只要满
的取法不唯一,只要满 足
足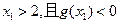 即可)
即可)(III)证明:由
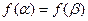 及(I)的结论知
及(I)的结论知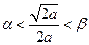 ,
,从而
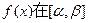 上的最小值为
上的最小值为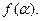 ……………………11分
……………………11分又由
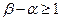 ,
,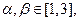 知
知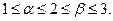
故
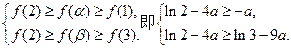 …………13分
…………13分从而
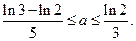 ……………………………………14分
……………………………………14分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
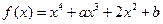 (
(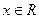 ),其中
),其中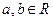 .
.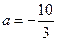 时,讨论函数
时,讨论函数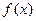 的单调性;
的单调性;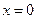 处有极值,求
处有极值,求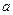 的取值范围;
的取值范围;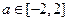 ,不等式
,不等式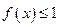 在
在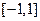 上恒成立,求
上恒成立,求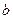 的取值范围.
的取值范围.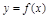 存在反函数,则方程
存在反函数,则方程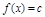 (
(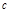 为常数)
为常数) 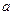 是实数,设函数
是实数,设函数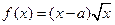
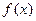 的单调性;
的单调性;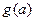 为函数
为函数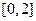 上的最小值
上的最小值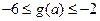
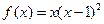 ,
,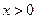 .
.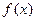 的极值;
的极值;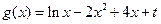 (
(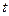 为常数),若使
为常数),若使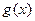 ≤
≤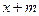 ≤
≤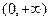 上恒成立的实数
上恒成立的实数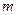 有且只有一个,求实数
有且只有一个,求实数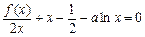 的解的个数,并说明理由.
的解的个数,并说明理由.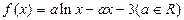
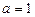 时,求函数
时,求函数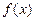 的单调区间;
的单调区间;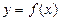 的图像在点
的图像在点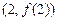 处的切线的倾斜角为
处的切线的倾斜角为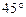 ,问:
,问: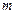 在什么范围取值时,函数
在什么范围取值时,函数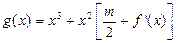 在区间
在区间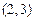 上总存在极值?
上总存在极值?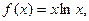
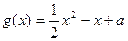 .
.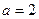 时,求
时,求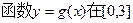 上的值域;
上的值域;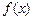 在
在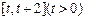 上的最小值;
上的最小值;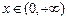 ,都有
,都有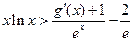 成立
成立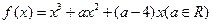 的导函数
的导函数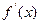 是偶函数,则曲线
是偶函数,则曲线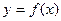 在原点处的切线方程是( )
在原点处的切线方程是( )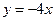
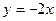
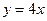
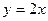
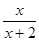 在点(-1,-1)处的切线方程为(......)
在点(-1,-1)处的切线方程为(......)