题目内容
17．cos120°+tan225°=$\frac{1}{2}$．分析 直接利用三角函数的诱导公式化简求值．
解答 解：cos120°+tan225°=cos（180°-60°）+tan（180°+45°）
=-cos60°+tan45°=-$\frac{1}{2}+1$=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．
点评 本题考查利用诱导公式求三角函数的值，是基础的计算题．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
8．某程序的框图如图所示，输入N=5，则输出的数等于（ ）
| A． | $\frac{5}{4}$ | B． | $\frac{5}{6}$ | C． | $\frac{6}{5}$ | D． | $\frac{4}{5}$ |
5．如图的程序是用来计算（ ）
| A． | 3×10的值 | B． | 1×2×3×…×10的值 | C． | 39的值 | D． | 310的值 |
9．
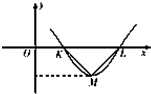设偶函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的部分图象如图所示，$\overrightarrow{MK}•\overrightarrow{ML}$=0，|KL|=1，|ML|=$\frac{{\sqrt{2}}}{2}$，则$f（\frac{1}{6}）$的值为（ ）
设偶函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的部分图象如图所示，$\overrightarrow{MK}•\overrightarrow{ML}$=0，|KL|=1，|ML|=$\frac{{\sqrt{2}}}{2}$，则$f（\frac{1}{6}）$的值为（ ）| A． | $-\frac{{\sqrt{3}}}{4}$ | B． | $-\frac{1}{4}$ | C． | $-\frac{1}{2}$ | D． | $\frac{{\sqrt{3}}}{4}$ |