题目内容
【题目】设函数![]()
当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
令![]() 其图象上任意一点
其图象上任意一点![]() 处切线的斜率
处切线的斜率![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
当![]() 时,令
时,令![]() 若
若![]() 与
与![]() 的图象有两个交点
的图象有两个交点![]() ,求证:
,求证:![]()
【答案】(1)单增区间为![]() 单减区间为
单减区间为![]() .(2)
.(2)![]() (3)见解析
(3)见解析
【解析】
试题(1)先求导函数,再求导函数在定义区间上零点,列表分析导函数符号变化规律,确定函调单调区间(2)先根据导数几何意义得不等式,再利用参变分离法将不等式转化为对应函数最值![]() 最大值 ,根据二次函数最值求得实数
最大值 ,根据二次函数最值求得实数![]() 的取值范围;(3)本小题较难,需作两次构造:一是消去a,构造以
的取值范围;(3)本小题较难,需作两次构造:一是消去a,构造以![]() 为自变量的函数
为自变量的函数![]() ,根据导数得其单调性,利用基本不等式得到
,根据导数得其单调性,利用基本不等式得到![]() 二是构造
二是构造![]() 利用导数易得单调性,可得
利用导数易得单调性,可得![]() ,即得
,即得![]()
试题解析:解:(1)![]() 定义域为
定义域为![]() ,
,
![]() ,
,
令![]() 解得
解得![]() ,令
,令![]() 解得
解得![]() ,
,
∴![]() 的单增区间为
的单增区间为![]() 单减区间为
单减区间为![]() .
.
(2)![]()
∴![]() 即
即![]()
令![]() ,∴
,∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ∴
∴![]() ,∴
,∴![]()
(3)![]() 定义域
定义域![]()
∴![]() ①,
①,![]() ②
②
①+②得![]() 即
即![]() ,③
,③
①-②得![]() 即
即![]() ,④
,④
由③④得![]() ,不妨设
,不妨设![]() ,记
,记![]() ,
,
令![]() ∴
∴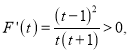
∴![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]()
∴![]() 即
即![]() ∴
∴![]()
∴
∴![]() 即
即![]()
令![]() ∴
∴![]() ∴
∴![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ∴
∴![]()
即![]() ∴
∴![]()

练习册系列答案
相关题目