题目内容
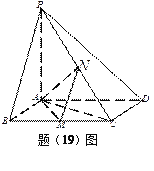
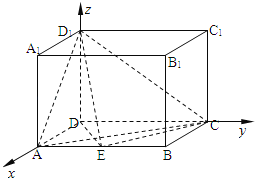
【题目】如图,长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,点E是线段AB中点.

(1)证明:D1E⊥CE;
(2)求二面角D1﹣EC﹣D的大小的余弦值;
(3)求A点到平面CD1E的距离.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据线面垂直的性质定理,证明CE⊥面D1DE即可证明:D1E⊥CE;
(2)建立坐标系,利用向量法即可求二面角D1﹣EC﹣D的大小的余弦值;
(3)根据点到平面的距离公式,即可求A点到平面CD1E的距离.
(1)证明:DD1⊥面ABCD,CE面ABCD;
所以DD1⊥CE,
Rt△DAE中,AD=1,AE=1,
DE![]() ,
,
同理:CE![]() ,又CD=2,CD2=CE2+DE2,
,又CD=2,CD2=CE2+DE2,
DE⊥CE,
DE∩CE=E,
所以,CE⊥面D1DE,
又D1E面D1EC,
所以,D1E⊥CE;
(2)设平面CD1E的法向量为![]() (x,y,z),
(x,y,z),
由(1)得![]() (1,1,﹣1),
(1,1,﹣1),![]() (1,﹣1,0)
(1,﹣1,0)
![]()
![]() x+y﹣1=0,
x+y﹣1=0,![]()
![]() x﹣y=0
x﹣y=0
解得:x=y![]() ,即
,即![]() (
(![]() ,
,![]() ,1);
,1);
又平面CDE的法向量为![]() (0,0,1),
(0,0,1),
∴cos![]() ,
,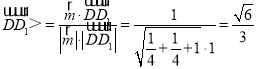 span>,
span>,
所以,二面角D1﹣EC﹣D的余弦值为![]() ;
;
(3)由(1)(2)知![]() (0,1,0),平面CD1E的法向量为
(0,1,0),平面CD1E的法向量为![]() (
(![]() ,
,![]() ,1);
,1);
故A点到平面CD1E的距离为d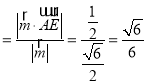 .
.

练习册系列答案
相关题目