题目内容
已知函数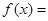
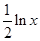
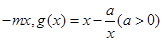 .
.
(I)求函数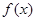 的单调区间;
的单调区间;
(Ⅱ)若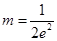 ,对
,对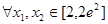 都有
都有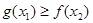 成立,求实数
成立,求实数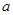 的取值范围;
的取值范围;
(Ⅲ)证明: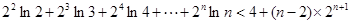 (
(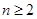 且
且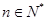 ).
).
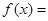
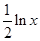
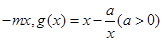 .
.(I)求函数
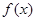 的单调区间;
的单调区间;(Ⅱ)若
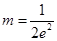 ,对
,对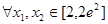 都有
都有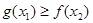 成立,求实数
成立,求实数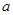 的取值范围;
的取值范围;(Ⅲ)证明:
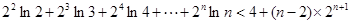 (
(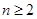 且
且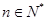 ).
).(I)当 时,
时,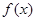 单调递增区间为(0,+∞).当m>0时,
单调递增区间为(0,+∞).当m>0时,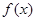 单调递增区间为(0,
单调递增区间为(0,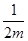 ),单调递减区间为(
),单调递减区间为(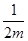 ,+∞). (Ⅱ)实数
,+∞). (Ⅱ)实数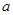 的取值范围为
的取值范围为 .(Ⅲ)详见解析.
.(Ⅲ)详见解析.
 时,
时,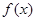 单调递增区间为(0,+∞).当m>0时,
单调递增区间为(0,+∞).当m>0时,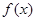 单调递增区间为(0,
单调递增区间为(0,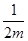 ),单调递减区间为(
),单调递减区间为(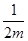 ,+∞). (Ⅱ)实数
,+∞). (Ⅱ)实数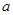 的取值范围为
的取值范围为 .(Ⅲ)详见解析.
.(Ⅲ)详见解析.试题分析:(I)应用导数研究函数的单调性.遵循“求导数,令导数大(小)于0,解不等式,求单调区间”.
(Ⅱ)将问题转化成“对


 都有
都有 ”,
”,通过求
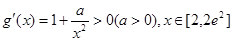 ,得到函数
,得到函数 在[2,2
在[2,2 ]上是增函数,
]上是增函数,求得
 =g(2)=2-
=g(2)=2- ,利用2-
,利用2-

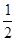 ,及
,及 得到实数
得到实数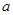 的取值范围为
的取值范围为 .
.(Ⅲ)通过构造函数
 ,利用(I)确定
,利用(I)确定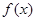 的单调性得到
的单调性得到 ,(当
,(当 时取“=”号),利用“错位相减法”求得S=
时取“=”号),利用“错位相减法”求得S=
证得
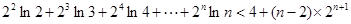 (
( ).
).试题解析:(I)

 1分
1分当
 时
时 ,
,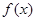 在(0,+∞)单调递增. 2分
在(0,+∞)单调递增. 2分当m>0时,由
 得
得
由
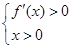 得
得
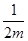
由
 得
得 >
>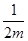 4分
4分综上所述:当
 时,
时,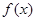 单调递增区间为(0,+∞).
单调递增区间为(0,+∞).当m>0时,
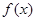 单调递增区间为(0,
单调递增区间为(0,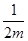 ),单调递减区间为(
),单调递减区间为(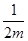 ,+∞). 5分
,+∞). 5分(Ⅱ)若m=
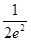 ,
, ,对
,对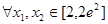 都有
都有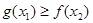 成立等价于对
成立等价于对

 都有
都有 6分
6分由(I)知在[2,2
 ]上
]上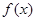 的最大值
的最大值 =
=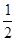 7分
7分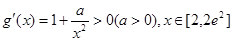
函数
 在[2,2
在[2,2 ]上是增函数,
]上是增函数, =g(2)=2-
=g(2)=2- , 9分
, 9分由2-


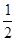 ,得
,得 ,又因为
,又因为 ,∴
,∴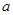 ∈
∈
所以实数
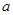 的取值范围为
的取值范围为 . 10分
. 10分(Ⅲ)证明:
 令m=
令m=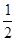 ,则
,则
由(I)知f(x)在(0,1)单调递增,(1,+∞)单调递减,
 ,(当x=1时取“=”号)
,(当x=1时取“=”号)
 11分
11分

<
 12分
12分令S=
 ①
①2S=
 ②
②①-②得-S=
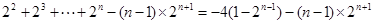
 S=
S=

 (
( ) 14分
) 14分
练习册系列答案
相关题目
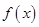 为奇函数,且当
为奇函数,且当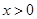 时,
时,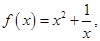 ,则
,则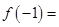 ( )
( )

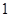
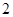
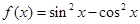 的最小正周期是
的最小正周期是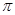 ;
;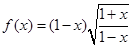 是偶函数;
是偶函数;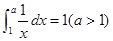 ,则
,则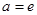 ;
;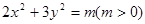 的离心率不确定。
的离心率不确定。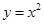 ;②
;②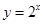 ;③
;③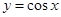 ;④
;④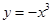 ,其中奇函数是( )
,其中奇函数是( ) 上的偶函数
上的偶函数 的周期为2,且当
的周期为2,且当 时,
时, ,则
,则 .
.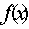 是定义域为
是定义域为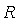 的偶函数,且
的偶函数,且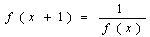 ,若
,若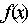 在
在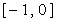 上是减函数,那么
上是减函数,那么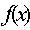 在
在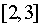 上是 ( )
上是 ( ) 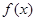 对任意
对任意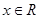 均满足
均满足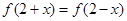 ,且当
,且当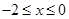 时,
时,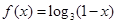 ,则
,则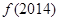 的值是 .
的值是 . 是定义在
是定义在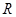 上的一个函数,则函数
上的一个函数,则函数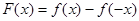 在
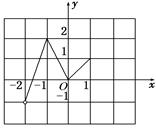
在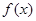 是定义在R上的周期为3的周期函数,如图表示该函数在区间(-2,1]上的图像,则
是定义在R上的周期为3的周期函数,如图表示该函数在区间(-2,1]上的图像,则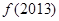 +
+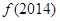 =( )
=( )